题目内容
【题目】如图，是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=4m，∠A=30°，则DE等于（ ）
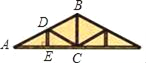
A. 1m B. 2m C. 3m D. 4m
【答案】A
【解析】分析: 利用直角三角形30°对的直角边等于斜边的一半，可得BC长，那么根据三角形中位线定理可得DE长应为BC长的一半．
详解: ：∵点D是斜梁AB的中点，立柱BC，DE垂直于横梁AC，
∴点E是AC的中点，
∴DE是直角三角形ABC的中位线，
根据三角形的中位线定理得：DE=
BC，
又∵在Rt△ABC中，AB=4m，∠A=30°，
∴BC=AB=2m．
故DE=BC=1m，
故选：A.
点睛: 本题考查了三角形中位线定理、直角三角形30°的角所对的边等于斜边的一半．解题的关键是证明DE是△ABC的中位线.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
