题目内容
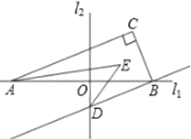
【题目】如图，点E，F在函数y= 
的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是 ． 
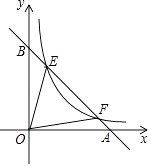
【答案】
【解析】解：作EP⊥y轴于P，EC⊥x轴于C，FD⊥x轴于D，FH⊥y轴于H，如图所示：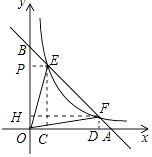
∵EP⊥y轴，FH⊥y轴，
∴EP//FH，
∴△BPE∽△BHF，
∴ 
= 
，即HF=3PE，
设E点坐标为（t， 
），则F点的坐标为（3t， 
），
∵S△OEF+S△OFD=S△OEC+S梯形ECDF ，
而S△OFD=S△OEC= 
×2=1，
∴S△OEF=S梯形ECDF= （ + ）（3t﹣t）= ；
所以答案是： ．
【考点精析】关于本题考查的比例系数k的几何意义，需要了解几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案．
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．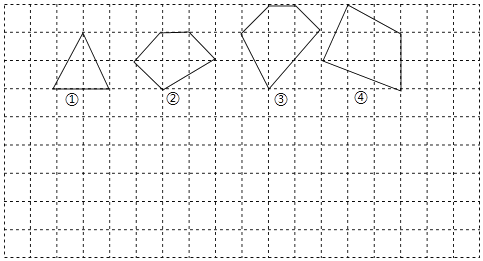
（1）根据图中提供的信息填表：
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=（用含m、n的代数式表示）
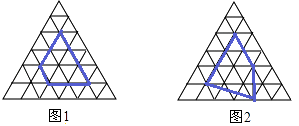
（2）对正三角形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，如图1、2是该正三角形格点中的两个多边形：设格点多边形的面积为S，该多边形各边上的格点个数之和为m，内部的格点个数为n，试探究S与m、n之间的关系式．则S与m、n之间的关系为S=（用含m、n的代数式表示）．
