题目内容
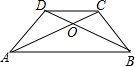如图，在梯形ABCD中，AB∥CD，AC和BD相交于点O，如果S△ODC：S△AOB=1：4，求S△ODC与S△AOD的比．分析：由于AB∥CD，根据三角形相似的判定方法得到△ODC∽△OBC，根据三角形相似的性质得到S△ODC：S△AOB=OC2：OA2=1：4，则OC：OA=1：2，然后根据同高的两三角形面积的比等于底边的比求解．
解答：解：∵AB∥CD，
∴△ODC∽△OBC，
∴S△ODC：S△AOB=OC2：OA2=1：4，
∴OC：OA=1：2，
∴S△ODC：S△AOD=OC：OA=1：2．
∴△ODC∽△OBC，
∴S△ODC：S△AOB=OC2：OA2=1：4，
∴OC：OA=1：2，
∴S△ODC：S△AOD=OC：OA=1：2．
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截的三角形与原三角形相似；相似三角形面积的比等于相似比的平方．也考查了三角形的面积公式．
练习册系列答案
阅读快车系列答案
相关题目
11、如图，在梯形ABCD中，AB∥CD，对角线AC、BD交于点O，则S△AOD
已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=CD=10．
如图，在梯形ABCD中，AD∥BC，AB⊥AD，对角线BD⊥DC．
20、如图，在梯形ABCD中，AD∥BC，并且AB=8，AD=3，CD=6，并且∠B+∠C=90°，则梯形面积S梯形ABCD=
如图，在梯形ABCD中，AD∥BC，∠BCD=90°，以CD为直径的半圆O切AB于点E，这个梯形的面积为21cm2，周长为20cm，那么半圆O的半径为（ ）| A、3cm | B、7cm | C、3cm或7cm | D、2cm |