Question

【题目】如图，已知正方形ABCD中，E是AD的中点，BF=CD+DF,若∠ABE为α，用含α的代数式表示∠CBF的度数是___________.

Answer 1

【答案】2α

【解析】

延长BC至点G使CG=DF，连接EG、BH，即可得出BF=BG，得到∠BFG=∠G，再通过证明△FDH≌△GCH可得H为CD和FG中点，易证△ABE≌△HBC，可得∠CBH=∠ABE=α，又因为在等腰三角形FBG中BH是△FBG中线，根据三线合一，BH也是∠FBC的角平分线，即可得到∠CBF=2α.

解：如图，延长延长BC至点G使CG=DF，连接EG、BH，

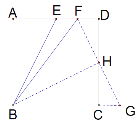
∵BF=CD+DF，BC=CD，CG=DF,

∴BF=BC+CG=BG；

在△FDH与△GCH中

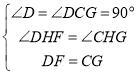
∴△FDH≌△GCH（AAS）

∴FH=GH,DH=CH,即H为FG、DC中点；

∵E为AD中点

∴AE=CH

在△ABE与△HBC中

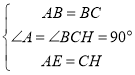
∴△ABE≌△HBC（SAS）

∴∠CBH=∠ABE=α

∵BF=BG，H为FG中点，

∴FG平分∠FBG（三线合一），

∴∠FBG=2∠CBH=2α.

故答案为：2α.