Question

【题目】综合与实践：

操作与发现：

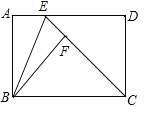
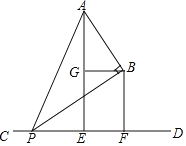
如图，已知A，B两点在直线CD的同一侧，线段AE，BF均是直线CD的垂线段，且BF在AE的右边，AE＝2BF，将BF沿直线CD向右平移，在平移过程中，始终保持∠ABP＝90°不变，BP边与直线CD相交于点P，点G是AE的中点，连接BG．

探索与证明：求证：

（1）四边形EFBG是矩形；

（2）△ABG∽△PBF．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）先通过等量代换得出GE＝BF，然后由AE⊥CD，BF⊥CD得出AE∥BF，从而得到四边形EFBG是平行四边形，最后利用BF⊥CD，则可证明平行四边形EFBG是矩形；

（2）先通过矩形的性质得出∠AGB＝∠GBF＝∠BFE＝90°，然后通过等量代换得出∠ABG＝∠PBF，再加上∠AGB＝∠PFB＝90°即可证明△ABG∽△PBF．

（1）证明：∵AE⊥CD，BF⊥CD，

∴AE∥BF，

∵AE＝2BF，

∴BF＝AE，

∵点G是AE的中点，

∴GE＝AE，

∴GE＝BF，又AE∥BF，

∴四边形EFBG是平行四边形，

∵BF⊥CD，

∴平行四边形EFBG是矩形；

（2）∵四边形EFBG是矩形，

∴∠AGB＝∠GBF＝∠BFE＝90°，

∵∠ABP＝90°，

∴∠ABP﹣∠GBP＝∠GBF﹣∠GBP，

即∠ABG＝∠PBF，

∵∠ABG＝∠PBF，∠AGB＝∠PFB＝90°，

∴△ABG∽△PBF．