Question

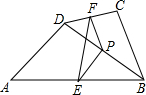
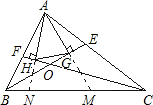
如图所示．△ABC中，∠B，∠C的平分线BE，CF相交于O，AG⊥BE于G，AH⊥CF于H．
（1）求证：GH∥BC；
（2）若AB=9厘米，AC=14厘米，BC=18厘米，求GH．

Answer 1

（1）证明：分别延长AG，AH交BC于M，N，在△ABM中，由已知，BG平分∠ABM，BG⊥AM，所以△ABG≌△MBG（ASA）．
从而，G是AM的中点．同理可证△ACH≌△NCH（ASA），
从而，H是AN的中点．所以GH是△AMN的中位线，从而，HG∥MN，即HG∥BC．

（2）由（1）知，△ABG≌△MBG及△ACH≌△NCH，
所以AB=BM=9厘米，AC=CN=14厘米．
又BC=18厘米，
所以BN=BC-CN=18-14=4（厘米），
MC=BC-BM=18-9=9（厘米）．
从而MN=18-4-9=5（厘米），
∴GH=

1

2

MN=

5

2

cm．