题目内容
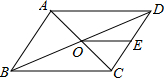
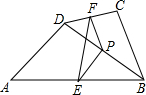
如图，在四边形ABCD中，AD=BC，点P是对角线的中点，点E和点F分别是CD与AB的中点．若∠PEF=20°，则∠EPF的度数是（ ）
| A．110° | B．120° | C．130° | D．140° |
∵在四边形ABCD中，P是对角线BD的中点，E，F分别是AB，CD的中点，
∴FP，PE分别是△CDB与△DAB的中位线，
∴PF=
BC，PE=
AD，
∵AD=BC，
∴PF=PE，故△EPF是等腰三角形．
∴∠PEF=∠PFE=20°，
∴∠EPF=180°-2∠PEF=140°．
故选：D．
∴FP，PE分别是△CDB与△DAB的中位线，
∴PF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=BC，
∴PF=PE，故△EPF是等腰三角形．
∴∠PEF=∠PFE=20°，
∴∠EPF=180°-2∠PEF=140°．
故选：D．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
