题目内容
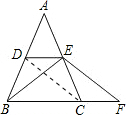
如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF=
BC.
(1)求证:DE=CF;(2)求证:BE=EF.

| 1 |
| 2 |
(1)求证:DE=CF;(2)求证:BE=EF.

证明:(1)∵D,E分别为AB,AC的中点,
∴DE为中位线.
∴DE∥BC,且DE=
BC.
又∵CF=
BC,
∴DE=CF.
(2)连接DC,
由(1)可得DE∥CF,且DE=CF,
∴四边形DCFE为平行四边形.
∴EF=DC.
∵AB=AC,且DE为中位线,
∴四边形DBCE为等腰梯形.
又∵DC,BE为等腰梯形DBCE的对角线,
∴DC=BE.
∴BE=EF.
∴DE为中位线.
∴DE∥BC,且DE=
| 1 |
| 2 |
又∵CF=
| 1 |
| 2 |
∴DE=CF.
(2)连接DC,
由(1)可得DE∥CF,且DE=CF,
∴四边形DCFE为平行四边形.
∴EF=DC.
∵AB=AC,且DE为中位线,
∴四边形DBCE为等腰梯形.
又∵DC,BE为等腰梯形DBCE的对角线,
∴DC=BE.
∴BE=EF.


练习册系列答案
相关题目