题目内容
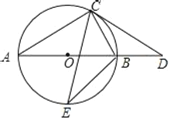
【题目】AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD.
(1)连接BC,求证:BC=OB;
(2)E是![]() 中点,连接CE,BE,若BE=2,求CE的长.
中点,连接CE,BE,若BE=2,求CE的长.
【答案】(1)见解析;(2)1+![]() .
.
【解析】
(1)连接OC,根据圆周角定理、切线的性质得到∠ACO=∠DCB,根据CA=CD得到∠CAD=∠D,证明∠COB=∠CBO,根据等角对等边证明;
(2)连接AE,过点B作BF⊥CE于点F,根据勾股定理计算即可.
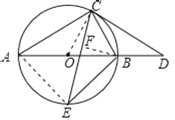
(1)证明:连接OC,
∵AB为⊙O直径,
∴∠ACB=90°,
∵CD为⊙O切线
∴∠OCD=90°,
∴∠ACO=∠DCB=90°﹣∠OCB,
∵CA=CD,
∴∠CAD=∠D.
∴∠COB=∠CBO.
∴OC=BC.
∴OB=BC;
(2)连接AE,过点B作BF⊥CE于点F,
∵E是AB中点,
∴![]() ,
,
∴AE=BE=2.
∵AB为⊙O直径,
∴∠AEB=90°.
∴∠ECB=∠BAE=45°,![]() ,
,
∴![]() .
.
∴CF=BF=1.
∴![]() .
.
∴![]() .
.

 考前必练系列答案
考前必练系列答案【题目】某校为了解九年级学生的体育达标情况,随机抽取![]() 名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
测试成绩(分) |
|
|
|
|
|
人数(人) |
|
|
|
|
|
(1)该校九年级有![]() 名学生,估计体育测试成绩为
名学生,估计体育测试成绩为![]() 分的学生人数;
分的学生人数;
(2)该校体育老师要对本次抽测成绩为![]() 分的甲、乙、丙、丁
分的甲、乙、丙、丁![]() 名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.