��Ŀ����
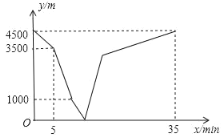
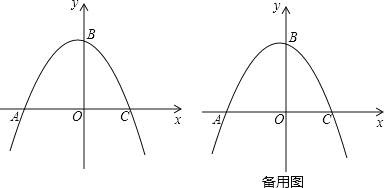
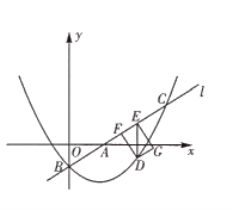
����Ŀ�����Ž�������н���Ŀ��ٷ�չ.ij�жԻ�ľ��������������ߣ�ij��רҵ���ƻ�Ͷ��15��Ԫ��ֲ���ܺ���ľ.�����г�������Ԥ�⣬��ֲ��ľ������y1(��Ԫ)��Ͷ����x(��Ԫ)����������ϵ����ͼ����ʾ����ֲ���ܵ�����y2(��Ԫ)��Ͷ����x(��Ԫ)�ĺ�����ϵ��ͼ����ʾ������OA�������ߵ�һ���֣�AΪ�����ߵĶ��㣻AB//x�ᣩ��
(1)���y1��y2����Ͷ����x�ĺ�����ϵʽ
(2)���רҵ����ֲ���ܺ���ľ��ȡ��������W(��Ԫ)����Ͷ����ֲ���ܵ��ʽ�t(��Ԫ)֮��ĺ�����ϵʽ:
(3)��רҵ��Ͷ����ֲ���ܵ��ʽ�Ϊ������Ԫʱ������ʹ��ȡ�����������������Ƕ���?

���𰸡���1��y1=2x��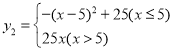 ����2��
����2��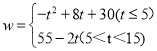 ����3����t=4ʱ��Wȡ�����ֵΪ46��.
����3����t=4ʱ��Wȡ�����ֵΪ46��.
��������
(1)��y2(��Ԫ)��Ͷ����x(��Ԫ)�ĺ�����ϵͼ��֪����0<x��5ʱy2��x�Ĺ�ϵʽͼ��Ϊ���κ���ͼ���һ���֣���x>5ʱ��y2=25����Ӧ�����������
(2)����(1)�������ϵʽ��y1=2x����Ͷ��15��Ԫ���г�����w��t�ĺ�����ϵʽ��
(3)��(2)��w��t�Ĺ�ϵʽ���w�����ֵ���ɣ�
�⣺(1)��y1=kx����ͼ����ʾ������y1=kx��ͼ���(1��2)��
����2=k1��k=2��������y1����Ͷ����x�ĺ�����ϵʽ��y1=2x��
�ɺ���ͼ���֪����x��5ʱ��y2��x�Ĺ�ϵʽͼ��Ϊ�����ߵ�һ���֣�
��������ߵĽ���ʽΪ��y2=a(x-5)2+25��
��(0��0)�������ʽ�ã�0=25a+25(x��5)�����a=-1��
�ʺ�������ʽΪy2=-(x-5)2+25(x��5)��
��x��5ʱ��y2=25(x��5����
��y2��x�Ĺ�ϵʽΪ ��
��
(2)��ΪͶ����ֲ����t��Ԫ����Ͷ����ֲ��ľ��15-t����Ԫ��
��t��5ʱ��y1=2(15-t)��y2=-(t-5)2+25��
��W=-(t-5)2+25+2(15-t)=-t2+8t+30��
��5��t��15ʱ��y1=2(15-t)��y2=25��
��W=55-2t��������W(��Ԫ)����Ͷ����ֲ���ܵ��ʽ�t(��Ԫ)֮��ĺ�����ϵʽ��
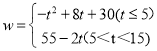
(3)��t��5ʱW=-t2+8t+30�����ݶ��κ��������ʣ���![]() ��Ԫʱ��Wȡ�����ֵ��W���ֵ=-42+8��4+30=-16+32+30=46��
��Ԫʱ��Wȡ�����ֵ��W���ֵ=-42+8��4+30=-16+32+30=46��
��5��t��15����-2��0��w��t���������С������t=5ʱ��w���ֵΪ45����45��46��
����t=4ʱ��Wȡ�����ֵΪ46��.
�ʴ�Ϊ��(1)y1=2x�� ��(2)
��(2)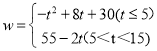 ����3����t=4ʱ��Wȡ�����ֵΪ46��.
����3����t=4ʱ��Wȡ�����ֵΪ46��.