题目内容
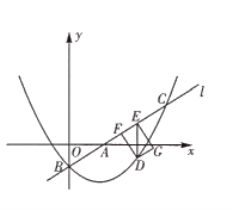
【题目】如图,已知直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 抛物线
抛物线![]() 经过点
经过点![]() 与直线
与直线![]() 的另一个交点为
的另一个交点为![]() .
.
![]() 求
求![]() 的值和抛物线的解析式
的值和抛物线的解析式
![]() 点
点![]() 在抛物线上,
在抛物线上,![]() 轴交直线
轴交直线![]() 于点
于点![]() 点
点![]() 在直线
在直线![]() 上,且四边形
上,且四边形![]() 为矩形.设点
为矩形.设点![]() 的横坐标为
的横坐标为![]() 矩形
矩形![]() 的周长为
的周长为![]() 求
求![]() 与
与![]() 的函数关系式以及
的函数关系式以及![]() 的最大值
的最大值
![]() 将
将![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别与
分别与![]() 点对应),若
点对应),若![]() 的两个顶点恰好落在抛物线上,请直接写出点
的两个顶点恰好落在抛物线上,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)n=2,![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 有最大值
有最大值![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)把点B坐标代入直线解析式求出m的值,再把点C坐标代入直线解析式即可求出n的值,然后利用待定系数法求出二次函数解析式;
(2)求出点A坐标,从而得到OA、OB长度,利用勾股定理求出AB,证明![]() 解直角三角形用DE表示出EF、DF,根据矩形周长公式表示p,利用直线和抛物线解析式表示出DE的长,整理即可的p与t的函数关系式,再利用二次函数性质求出p的最大值;
解直角三角形用DE表示出EF、DF,根据矩形周长公式表示p,利用直线和抛物线解析式表示出DE的长,整理即可的p与t的函数关系式,再利用二次函数性质求出p的最大值;
(3)将![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() ,可得A1O1
,可得A1O1![]() y轴,B1O1
y轴,B1O1![]() x轴,可得两种情况.当B1、O1在抛物线上时,根据B1O1=1,利用抛物线对称性,求出O1横坐标,进而求出A1坐标;当
x轴,可得两种情况.当B1、O1在抛物线上时,根据B1O1=1,利用抛物线对称性,求出O1横坐标,进而求出A1坐标;当![]() 在抛物线上时,表示出A1,O1坐标,由A1O1=
在抛物线上时,表示出A1,O1坐标,由A1O1=![]() ,从而求得A1坐标
,从而求得A1坐标
解:![]() 直线
直线![]() 经过点
经过点![]()
![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 直线
直线![]() 经过点
经过点![]()
![]()
![]() .
.
![]() 抛物线
抛物线![]() 经过点
经过点![]() 和点
和点![]() ,
,
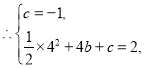 解得
解得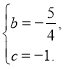
抛物线的解析式为![]()
![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]()
![]()
![]()
![]()

![]() 轴,
轴,
![]() .
.
又![]() ,
,
![]()
![]()
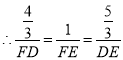
![]()
![]()
![]() 点
点![]() 在抛物线上,点
在抛物线上,点![]() 的横坐标为
的横坐标为![]()
![]()
![]() ,且
,且![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 有最大值
有最大值![]()
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]()
![]() 绕平面内某点
绕平面内某点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别与点
分别与点![]() 对应),且
对应),且![]() 的两个顶点恰好落在抛物线上,
的两个顶点恰好落在抛物线上,
![]() 存在顶点
存在顶点![]() 落在抛物线上或顶点
落在抛物线上或顶点![]() 落在抛物线上两种可能的情况.
落在抛物线上两种可能的情况.
![]() 点
点![]() 恰好都落在抛物线上时,如图1,
恰好都落在抛物线上时,如图1,

则![]() 轴,
轴,![]() 轴,
轴,
![]() 点
点![]() 关于抛物线的对称轴对称
关于抛物线的对称轴对称

![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]()
![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]()
当![]() 时,
时,
![]()
![]() ,
,
![]() 点
点![]() 的纵坐标为
的纵坐标为![]()
![]()
![]() 当点
当点![]() 恰好都落在抛物线上时,如图2.
恰好都落在抛物线上时,如图2.
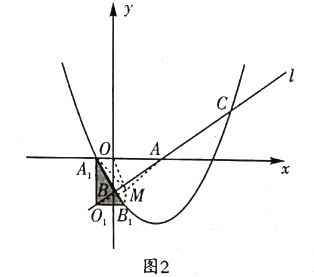
设![]()
![]() ,
,![]()
![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]()
![]()
综上,点![]() 的坐标为
的坐标为![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案【题目】为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
15名男生测试成绩统计如下:(满分100分)78,90,99,93,92,95,94,100,90,85,86,95,75,88,90
15名女生测试成绩统计如下:(满分100分)77,82,83,86,90,90,92,91,93,92,92,92,92,98,100
(整理、描述数据)
70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 | 95.5~100.5 | |
男生 | 1 | 1 | 1 | 5 | 5 | 2 |
女生 | 0 | 1 | 2 | 3 | 7 | 2 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
性别 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 90 | 90 | 90 | 44.9 |
女生 | 90 |
|
| 32.8 |
在表中:![]() ________.
________.![]() ________;
________;
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人?
(3)通过数据分析得到的结论,你认为男生和女生中谁的成绩比较好?请说明理由.