ΧβΡΩΡΎ»ί
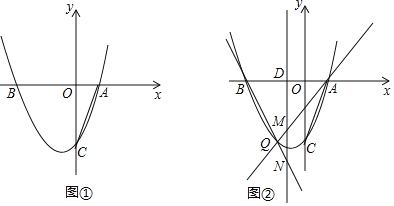
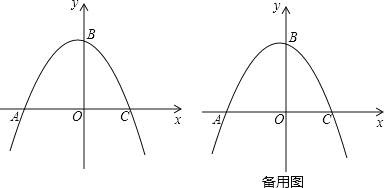
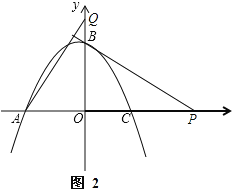
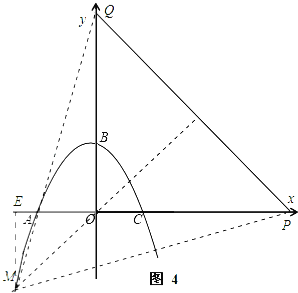
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏΨ≠ΙΐA(©¹2Θ§0)Θ§B(0Θ§2)Θ§C(![]() Θ§0)»ΐΒψΘ§“ΜΕ·ΒψP¥”‘≠Βψ≥ωΖΔ“‘1ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»―Ίx÷α’ΐΖΫœρ‘ΥΕ·Θ§Ν§Ϋ”BPΘ§ΙΐΒψAΉς÷±œΏBPΒΡ¥ΙœΏΫΜy÷α”ΎΒψQΘ°…ηΒψPΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ°
Θ§0)»ΐΒψΘ§“ΜΕ·ΒψP¥”‘≠Βψ≥ωΖΔ“‘1ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»―Ίx÷α’ΐΖΫœρ‘ΥΕ·Θ§Ν§Ϋ”BPΘ§ΙΐΒψAΉς÷±œΏBPΒΡ¥ΙœΏΫΜy÷α”ΎΒψQΘ°…ηΒψPΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ°
(1)«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
(2)Β±BQ=![]() AP ±Θ§«σtΒΡ÷ΒΘΜ
AP ±Θ§«σtΒΡ÷ΒΘΜ
(3)ΥφΉ≈ΒψPΒΡ‘ΥΕ·Θ§≈ΉΈοœΏ…œ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ ΙΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥tΒΡ÷ΒΦΑœύ”ΠΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1) y=©¹![]() x2©¹
x2©¹![]() x+2 ΘΜ(2) t=
x+2 ΘΜ(2) t=![]() Μρ6 ±Θ§BQ=
Μρ6 ±Θ§BQ=![]() APΘΜ(3) Β±t=
APΘΜ(3) Β±t=![]() ©¹1 ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(1Θ§1)ΘΜΒ±t=3+3
©¹1 ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(1Θ§1)ΘΜΒ±t=3+3![]() ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(©¹3Θ§©¹3)Θ°
±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(©¹3Θ§©¹3)Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο¥ζ»κœΒ ΐΖ®Θ§ΫΪ3ΒψΉχ±ξ¥ζ»κΩ…«σΒΟΘΜ
Θ®2Θ©¥φ‘Ύ2÷÷«ιΩωΘ§ΒψQ‘ΎΒψBΒΡœ¬ΖΫΚΆ…œΖΫΘ§άϊ”ΟBQ=![]() AP“Ή«σΒΟtΒΡ÷ΒΘΜ
AP“Ή«σΒΟtΒΡ÷ΒΘΜ
Θ®3Θ©œ»÷ΛΓςAOQΓ’ΓςBOPΘ§ΒΟΒΫΓςOPQΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΒΟMΒψ±Ί‘ΎPQΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§Φ¥M‘Ύy=x…œΘ§ΝΣΝΔΒψM‘Ύ≈ΉΈοœΏ…œΒΡΖΫ≥ΧΘ§ΫβΒΟM”–2÷÷«ιΩωΘ§ΉνΚσάϊ”ΟΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΒΡΦΗΚΈ–‘÷ Ζ÷Έω«σΫβΦ¥Ω…Θ°
ΫβΘΚ(1)…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=ax2+bx+cΘ§
ΓΏ≈ΉΈοœΏΨ≠ΙΐA(©¹2Θ§0)Θ§B(0Θ§2)Θ§C(![]() Θ§0)»ΐΒψΘ§
Θ§0)»ΐΒψΘ§
Γύ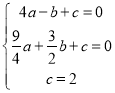 Θ§
Θ§
ΫβΒΟ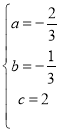 Θ§
Θ§
Γύy=![]() x2
x2![]() x+2Θ°
x+2Θ°
(2)ÿAQâPBȧBOâAPȧ
ΓύΓœAOQ=ΓœBOP=90ΓψΘ§ΓœPAQ=ΓœPBOΘ§
ΓΏAO=BO=2Θ§
ΓύΓςAOQΓ’ΓςBOPΘ§
ΓύOQ=OP=tΘ°
ΔΌ»γΆΦ1Θ§Β±tΓή2 ±Θ§ΒψQ‘ΎΒψBœ¬ΖΫΘ§¥Υ ±BQ=2©¹tΘ§AP=2+tΘ°
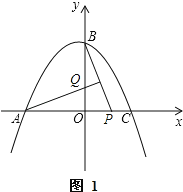
ÿBQ=![]() APȧ
APȧ
Γύ2©¹t=![]() (2+t)Θ§
(2+t)Θ§
Γύt=![]() Θ°
Θ°
ΔΎ»γΆΦ2Θ§Β±tΘΨ2 ±Θ§ΒψQ‘ΎΒψB…œΖΫΘ§¥Υ ±BQ=t©¹2Θ§AP=2+tΘ°
ÿBQ=![]() APȧ
APȧ
Γύt©¹2=![]() (2+t)Θ§
(2+t)Θ§
Γύt=6Θ°
Ήέ…œΥυ ωΘ§t=![]() Μρ6 ±Θ§BQ=
Μρ6 ±Θ§BQ=![]() APΘ°
APΘ°
(3)Β±t=![]() ©¹1 ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(1Θ§1)ΘΜΒ±t=3+3
©¹1 ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(1Θ§1)ΘΜΒ±t=3+3![]() ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(©¹3Θ§©¹3)Θ°
±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(©¹3Θ§©¹3)Θ°
Ζ÷Έω»γœ¬ΘΚ
ÿAQâBPȧ
ΓύΓœQAO+ΓœBPO=90ΓψΘ§
ΓΏΓœQAO+ΓœAQO=90ΓψΘ§
ΓύΓœAQO=ΓœBPOΘ°
‘ΎΓςAOQΚΆΓςBOP÷–Θ§
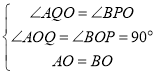 Θ§
Θ§
ΓύΓςAOQΓ’ΓςBOPΘ§
ΓύOP=OQΘ§
ΓύΓςOPQΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓΏΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΘ§‘ρMΒψ±Ί‘ΎPQΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ§
ΓΏ÷±œΏy=x¥Ι÷±ΤΫΖ÷PQΘ§
ΓύM‘Ύy=x…œΘ§…ηM(xΘ§y)Θ§
Γύ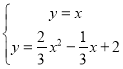 Θ§
Θ§
ΫβΒΟ![]() Μρ
Μρ![]() Θ§
Θ§
ΓύMΒψΩ…ΡήΈΣ(1Θ§1)Μρ(©¹3Θ§©¹3)Θ°
ΔΌ»γΆΦ3Θ§Β±MΒΡΉχ±ξΈΣ(1Θ§1) ±Θ§ΉςMDΓΆx÷α”ΎDΘ§
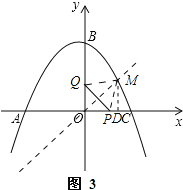
‘ρ”–PD=|1©¹t|Θ§MP2=1+|1©¹t|2=t2©¹2t+2Θ§PQ2=2t2Θ§
ΓΏΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύMP=PQΘ§
Γύt2+2t©¹2=0Θ§
Γύt=©¹1+![]() Θ§t=©¹1©¹
Θ§t=©¹1©¹![]() (ΗΚ÷Β…α»Ξ)Θ°
(ΗΚ÷Β…α»Ξ)Θ°
ΔΎ»γΆΦ4Θ§Β±MΒΡΉχ±ξΈΣ(©¹3Θ§©¹3) ±Θ§ΉςMEΓΆx÷α”ΎEΘ§
‘ρ”–PE=3+tΘ§ME=3Θ§
ΓύMP2=32+(3+t)2=t2+6t+18Θ§PQ2=2t2Θ§
ΓΏΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύMP=PQΘ§
Γύt2©¹6t©¹18=0Θ§
Γύt=3+3![]() Θ§t=3©¹3
Θ§t=3©¹3![]() (ΗΚ÷Β…α»Ξ)Θ°
(ΗΚ÷Β…α»Ξ)Θ°
Ήέ…œΥυ ωΘ§Β±t=©¹1+![]() ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(1Θ§1)Θ§ΜρΒ±t=3+3
±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(1Θ§1)Θ§ΜρΒ±t=3+3![]() ±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(©¹3Θ§©¹3)Θ§ ΙΒΟΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΘ°
±Θ§≈ΉΈοœΏ…œ¥φ‘ΎΒψM(©¹3Θ§©¹3)Θ§ ΙΒΟΓςMPQΈΣΒ»±Ώ»ΐΫ«–ΈΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
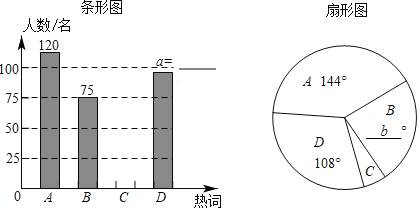
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΈΣΝΥΝΥΫβ―ß…ζΕ‘ΓΑ‘ΛΖά–¬–ΆΙΎΉ¥≤ΓΕΨΓ±÷Σ ΕΒΡ’ΤΈ’«ιΩωΘ§―ß–ΘΉι÷·ΝΥ“Μ¥ΈœΏ…œ÷Σ Ε≈ύ―ΒΘ§≈ύ―ΒΫα χΚσΫχ––≤β ‘Θ§‘Ύ»Ϊ–Θ2000Οϊ―ß…ζ÷–Θ§Ζ÷±π≥ι»ΓΝΥΡ–…ζΘ§≈°…ζΗς15Ζί≥…Φ®Θ§’ϊάμΖ÷ΈωΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘ°
Θ® ’Φ· ΐΨίΘ©
15ΟϊΡ–…ζ≤β ‘≥…Φ®Ά≥ΦΤ»γœ¬ΘΚΘ®¬ζΖ÷100Ζ÷Θ©78Θ§90Θ§99Θ§93Θ§92Θ§95Θ§94Θ§100Θ§90Θ§85Θ§86Θ§95Θ§75Θ§88Θ§90
15Οϊ≈°…ζ≤β ‘≥…Φ®Ά≥ΦΤ»γœ¬ΘΚΘ®¬ζΖ÷100Ζ÷Θ©77Θ§82Θ§83Θ§86Θ§90Θ§90Θ§92Θ§91Θ§93Θ§92Θ§92Θ§92Θ§92Θ§98Θ§100
Θ®’ϊάμΓΔΟη ω ΐΨίΘ©
70.5ΓΪ75.5 | 75.5ΓΪ80.5 | 80.5ΓΪ85.5 | 85.5ΓΪ90.5 | 90.5ΓΪ95.5 | 95.5ΓΪ100.5 | |
Ρ–…ζ | 1 | 1 | 1 | 5 | 5 | 2 |
≈°…ζ | 0 | 1 | 2 | 3 | 7 | 2 |
Θ®Ζ÷Έω ΐΨίΘ©
Θ®1Θ©ΝΫΉι―υ±Ψ ΐΨίΒΡΤΫΨυ ΐΓΔ÷Ύ ΐΓΔ÷–ΈΜ ΐΓΔΖΫ≤ν»γœ¬±μΥυ ΨΘΚ
–‘±π | ΤΫΨυ ΐ | ÷Ύ ΐ | ÷–ΈΜ ΐ | ΖΫ≤ν |
Ρ–…ζ | 90 | 90 | 90 | 44.9 |
≈°…ζ | 90 |
|
| 32.8 |
‘Ύ±μ÷–ΘΚ![]() ________Θ°
________Θ°![]() ________ΘΜ
________ΘΜ
Θ®2Θ©»τΙφΕ®ΒΟΖ÷‘Ύ80Ζ÷“‘…œΘ®≤ΜΚ§80Ζ÷Θ©ΈΣΚœΗώΘ§«κΙάΦΤ»Ϊ–Θ―ß…ζ÷–ΓΑ‘ΛΖά–¬–ΆΙΎΉ¥≤ΓΕΨΓ±÷Σ Ε≤β ‘ΚœΗώΒΡ―ß…ζ”–Εύ…Ό»ΥΘΩ
Θ®3Θ©Ά®Ιΐ ΐΨίΖ÷ΈωΒΟΒΫΒΡΫα¬έΘ§Ρψ»œΈΣΡ–…ζΚΆ≈°…ζ÷–Υ≠ΒΡ≥…Φ®±»ΫœΚΟΘΩ«κΥΒΟςάμ”…Θ°