题目内容
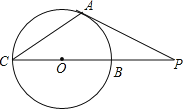
【题目】如图,PA切⊙O于点A,PC过点O且与⊙O交于B,C两点,若PA=6cm,PB=2![]() cm,则△PAC的面积是_____cm2.
cm,则△PAC的面积是_____cm2.
【答案】9![]()
【解析】
连接OA,先在Rt△OAP中,利用勾股定理求得AD、AO的长,然后求出CB的长,进而得到CP的长,最终求得面积.
解:如图,连接OA,过点A作AD⊥BC于点D,
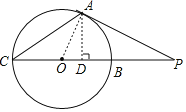
设⊙O的半径为x,
则OB=OA=x,
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°,
∴在Rt△AOP中,PA=6,OP=x+2![]() ,OA=x,
,OA=x,
根据勾股定理,得
PA2+OA2=OP2,
即36+x2=(x+2![]() )2,
)2,
解得x=2![]() ,
,
∴OA=OB=OC=2![]() ,
,
∴OP=4![]() ,
,
∴∠P=30°,
∴AD=![]() AP=3,
AP=3,
∴S△PAC=![]() PCAD=
PCAD=![]() 6
6![]() ×3=9
×3=9![]() (cm2).
(cm2).
∴△PAC的面积为9![]() cm2.
cm2.
故答案为:9![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?