题目内容
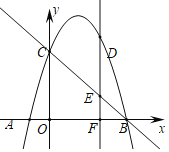
【题目】已知二次函数![]() 的图象经过三点(1,0),(-3,0),(0,
的图象经过三点(1,0),(-3,0),(0,![]() ).
).
(1)求该二次函数的解析式;
(2)若反比例函数![]() 图像与二次函数
图像与二次函数![]() 的图像在第一象限内交于点
的图像在第一象限内交于点![]() ,
, ![]() 落在两个相邻的正整数之间,请写出这两个相邻的正整数;
落在两个相邻的正整数之间,请写出这两个相邻的正整数;
(3)若反比例函数![]() 的图像与二次函数
的图像与二次函数![]() 的图像在第一象限内的交点为A,点A的横坐标为
的图像在第一象限内的交点为A,点A的横坐标为![]() 满足
满足![]() ,试求实数
,试求实数![]() 的取值范围.
的取值范围.
【答案】(1)y=![]() ;(2)1与2;(3)
;(2)1与2;(3)![]()
【解析】
(1)已知了抛物线与x轴的交点,可用交点式来设二次函数的解析式.然后将另一点的坐标代入即可求出函数的解析式.
(2)根据(1)的抛物线的解析式和反比例函数的解析式的图象交点,即可得出符合条件的x0的值,进而可写出所求的两个正整数.
(3)点A的横坐标x0满足2<x0<3,可通过x=2,x=3两个点上抛物线与反比例函数的大小关系即可求出k的取值范围.
(1)设抛物线解析式为y=a(x-1)(x+3)
将(0,-![]() )代入,解得a=
)代入,解得a=![]() .
.
∴抛物线解析式为y=![]()
(2)根据函数图像可知交点的横坐标x0 落在1和2之间,从而得出这两个相邻的正整数为1与2
(3)由函数图像或函数性质可知:当2<x<3时,
对y1=![]() , y1随着x增大而增大,对y2=
, y1随着x增大而增大,对y2=![]() (k>0),
(k>0),
y2随着X的增大而减小.因为A(X0,Y0)为二次函数图像与反比例函数图像的交点,所以当X0=2时,由反比例函数图象在二次函数上方得y2>y1,
得![]()
同理,当X0=3时,由二次函数数图象在反比例上方得y1>y2,
得K<12
所以K的取值范围为![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目