Question

【题目】如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，点D在AB边上，△CDE是等边三角形．

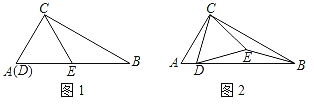
（1）如图1，当点E在AB边上时，CE与BE有何数量关系，请说明理由；

（2）如图2，当点E在△ABC内时，猜想CE与BE的数量关系，并加以证明；

（3）再另画一种情况，写出相应结论．（不用证明）

Answer 1

【答案】（1）CE＝BE，理由详见解析；（2）CE＝BE，证明详见解析；（3）详见解析

【解析】

（1）证出∠BCE＝∠ABC，即可得出CE＝BE；

（2）取AB的中点O，连接OC、OE，证△ACD≌△OCE（SAS），得出∠A＝∠COE，证出∠COE＝∠BOE，证△COE≌△BOE（SAS），即可得出CE＝BE；

（3）当点E在△ABC外时，CE＝BE成立；取AB的中点O，连接OC、OE，同（2）得△ACD≌△OCE（SAS），得出∠A＝∠COE＝60°，证出∠COE＝∠BOE，证△COE≌△BOE（SAS），即可得出CE＝BE．

解：（1）CE＝BE，理由如下：

∵△CDE是等边三角形，

∴∠ACE＝60°，

∵∠ACB＝90°，

∴∠BCE＝90°﹣60°＝30°，

∵∠ABC＝30°，

∴∠BCE＝∠ABC，

∴CE＝BE；

（2）CE＝BE，理由如下：

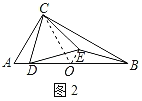
取AB的中点O，连接OC、OE，如图2所示：

∵∠ACB＝90°，

∴OC＝AB＝OA＝OB，

∵∠ABC＝30°，

∴∠A＝60°，

∴△AOC是等边三角形，

∴AC＝OC，∠AOC＝∠ACO＝60°，

∴AC＝OC＝OB，

∵△CDE是等边三角形，

∴CD＝CE，∠DCE＝60°，

∴∠ACO＝∠DCE，

∴∠ACD＝∠OCE，

在△ACD和△OCE中，

，

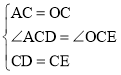∴△ACD≌△OCE（SAS），

∴∠A＝∠COE，

∵∠AOC＝60°，

∴∠BOE＝180°﹣60°﹣60°＝60°，

∴∠COE＝∠BOE，

在△COE和△BOE中，

，

∴△COE≌△BOE（SAS），

∴CE＝BE；

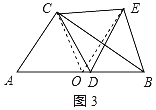
（3）如图3，当点E在△ABC外时，CE＝BE成立；理由如下：

取AB的中点O，连接OC、OE，

同（2）得：△ACD≌△OCE（SAS），

∴∠A＝∠COE＝60°，

∴∠BOE＝180°﹣60°﹣60°＝60°，

∴∠COE＝∠BOE，

在△COE和△BOE中，

，

∴△COE≌△BOE（SAS），

∴CE＝BE．