Question

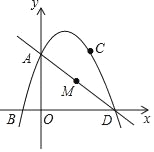
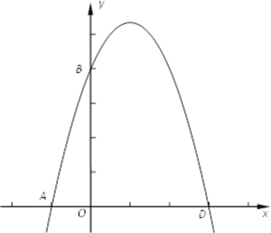
【题目】如图，在平面直角坐标系中，己知二次函数的图像与y轴交于点B(0， 4)，与x轴交于点A(－1，0)和点D．

(1)求二次函数的解析式；

(2)求抛物线的顶点和点D的坐标；

(3)在抛物线上是否存在点P，使得△BOP的面积等于？如果存在，请求出点P的坐标？如果不存在，请说明理由．

Answer 1

【答案】（1）；（2）D的坐标为（3，0），顶点坐标为（1，）；（3）满足条件的点P有两个，坐标分别为P1(，)、P2()．

【解析】

（1）利用待定系数法求出二次函数解析式即可；
（2）根据二次函数的解析式得点D的坐标，将解析式化为顶点式可得顶点的坐标；
（3）设P的坐标为P（x，y），到y轴的距离为|x|，则S△BOP=BO|x|，解出x=±，进而得出P点坐标．

解：(1)把点A(－1，0)和点B(0， 4)代入二次函数中得：

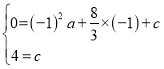
解得：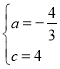

所以二次函数的解析式为： ；

（2）根据（1）得点D的坐标为（3，0），

=，

∴顶点坐标为（1，）；

(3)存在这样的点P，设P的坐标为P(x，y)，到y轴的距离为∣x∣

∵ S△BOP＝BO∣x∣

∴＝×4∣x∣

解得：∣x∣＝所以x＝±

把x＝代入中得：

即：y＝，

把x＝－代入中得：

即：y＝－

∴满足条件的点P有两个，坐标分别为P1(，)、P2()．