Question

【题目】如图，在平面直角坐标系中，一次函数y＝﹣x+m（m为常数）的图象与x轴交于A（﹣3，0），与y轴交于点C．以直线x＝﹣1为对称轴的抛物线y＝ax2+bx+c（a，b，c为常数，且a＞0）经过A，C两点，与x轴正半轴交于点B．
（1）求一次函数及抛物线的函数表达式；

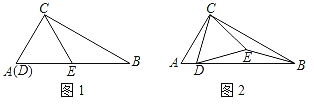
（2）P为线段AC上的一个动点（点P与C、A不重合）过P作x轴的垂线与这个二次函数的图象交于点D，连接CD，AD，点P的横坐标为n，当n为多少时，△CDA的面积最大，最大面积为多少？

（3）在对称轴上是否存在一点E，使∠ACB＝∠AEB？若存在，求点E的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝﹣x﹣2，；（2）时，△CDA的面积最大，最大面积是；（3）E1（﹣1，﹣），E2（﹣1，）．

【解析】

(1)根据待定系数法即可直接求出一次函数解析式，根据A点坐标和对称轴求出B点坐标，利用交点式即可求出二次函数解析式；

(2)用n可表示P点和D点坐标，则△CDA的面积为PDOA，得到关于n的二次函数表达式，由二次函数的性质可求出面积的最大值；

(3)作△ABC的外接圆⊙M，⊙M与直线x＝﹣1位于x轴下方部分的交点为E1，E1关于x轴的对称点为E2，则E1、E2均为所求的点，可求出M点的坐标，再由勾股定理求出FE1的长，则点E1的坐标可求出，由对称性可求得E2的坐标．

(1)∵y＝﹣x+m经过点A(﹣3，0)，

∴0＝2+m，解得m＝﹣2，

∴直线AC解析式为y＝﹣x﹣2，

∴C(0，﹣2)，

∵抛物线y＝ax2+bx+c对称轴为x＝﹣1，且与x轴交于A(﹣3，0)，

∴另一交点为B(1，0)，设抛物线解析式为y＝a(x+3)(x﹣1)，

∵抛物线经过 C(0，﹣2)，

∴﹣2＝a3×(﹣1)，解得a＝，

∴抛物线解析式为y＝x2+x﹣2；

(2)如图1，设P(n，-n-2)，D(n，n2+n﹣2)，

∴PD＝-n-2-(n2+n﹣2)= -n2-2n，

∴S△CDA=S△APD+S△PDC=PDOA=×3(-n2-2n)=-n2-3n=-(n+)2+，

∴n=时，△CDA的面积最大，最大面积是；

(3)如图2，设直线x＝﹣1与x轴的交点为点F，作△ABC的外接圆⊙M，⊙M与直线x＝﹣1位于x轴下方部分的交点为E1，E1关于x轴的对称点为E2，则E1、E2均为所求的点．

∵∠AE1B、∠ACB都是弧AB所对的圆周角，

∴∠AE1B＝∠ACB，且射线FM上的其它点E都不满足∠AEB＝∠ACB．

∵圆心M必在AB边的垂直平分线即直线x＝﹣1上．

∴点M的横坐标为﹣1．

∵B(1，0)，C(0，﹣2)，

∴设直线BC的解析式为y＝kx+b，

∴，解得，

直线BC的解析式为y＝2x﹣2，

∴直线BC的中垂线的解析式为y＝﹣x+m，由直线经过点(，-1)，

∴m＝-，

∴直线BC的中垂线的解析式为y＝﹣x﹣，

∵点M在直线y＝﹣x﹣上，

∴y=﹣﹣=-，

∴M(-1，-)，

∴MA＝，

∴FE1＝=，

∴E1(﹣1，﹣)，

由对称性得E2(﹣1，)，

∴符合题意的点E的坐标为E1(﹣1，﹣)，E2(﹣1，)．