Question

【题目】一所中学九年级240名同学参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树数量，所分四个类别为，A：植4棵；B：植5棵；C：植6棵；D：植7棵．将各类别人数绘制成扇形图和条形图．经确认扇形图是正确的，而条形图尚有一处错误．

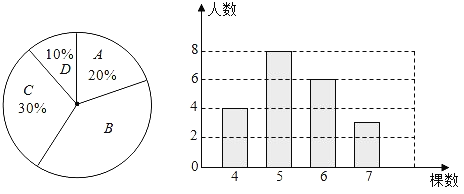
（1）指出条形图中存在的错误，并说明理由．

（2）指出样本的众数、中位数．

（3）估计在全年级随机抽取1人，植树5棵的概率．

（4）估计全年级240名同学这次共植树多少棵．（精确到10棵）

Answer 1

【答案】（1）D错误，理由详见解析；（2）众数：5；中位数：5；（3）0.4；（4）1270

【解析】

（1）利用总人数乘对应的百分比求解即可；

（2）根据众数、中位数的定义即可直接求解；

（3）计算样本植树5棵的百分比后即可确定概率；

（4）计算样本平均数后即可求得答案．

解：（1）D错误，理由：20×10%＝2≠3；

（2）由题意可知，植树5棵人数最多，故众数为5，

共有20人植树，其中位数是第10、11人植树数量的平均数，

即（5+5）＝5，故中位数为5；

（3）样本植树5棵的百分比为1﹣（20%+30%+10%）＝40%，

估计在全年级随机抽取1人，植树5棵的概率是0.4；

（4）样本平均数为（4×4+5×8+6×6+7×2）＝5.3，

估计240名同学这次共植树5.3×240＝1272≈1270（棵）．