题目内容
【题目】已知Rt△ABC中,∠C=90°,AC=BC,直线m经过点C,分别过点A,B作直线m的垂线,垂足分别为点E,F,若AE=3,AC=5,则线段EF的长为_______.
【答案】1或7
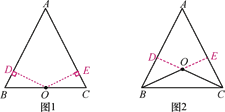
【解析】分两种情况:①如图1所示:先证出∠1=∠3,由勾股定理求出CE,再证明△BCF≌△CAE,得出对应边相等CF=AE=3,得出EF=CE-CF即可;
②如图2所示:先证出∠1=∠3,由勾股定理求出CE,再证明△BCF≌△CAE,得出对应边相等CF=AE=3,得出EF=CE+CF即可.
分两种情况:①如图1所示:
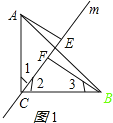
∵∠ACB=90°,
∴∠1+∠2=90°,
∵BF⊥m,
∴∠BFC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵AE⊥m,
∴∠AEC=90°,
∴CE=![]() =4,
=4,
在△BCF和△CAE中,
 ,
,
∴△BCF≌△CAE(AAS),
∴CF=AE=3,
∴EF=CE-CF=4-3=1;
②如图2所示:

∵∠ACB=90°,
∴∠1+∠2=90°,
∵BF⊥m,
∴∠BFC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵AE⊥m,
∴∠AEC=90°,
∴CE=![]() =4,
=4,
在△BCF和△CAE中,
 ,
,
∴△BCF≌△CAE(AAS),
∴CF=AE=3,
∴EF=CE+CF=4+3=7;
综上所述:线段EF的长为:1或7.
故答案为:1或7.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目