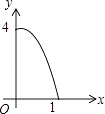Question

【题目】如图，已知关于x的二次函数y=x2+mx的图象经过原点O，并且与x轴交于点A，对称轴为直线x=1．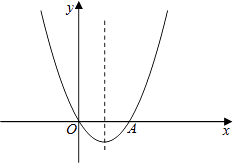
（1）常数m= ， 点A的坐标为；
（2）若关于x的一元二次方程x2+mx=n（n为常数）有两个不相等的实数根，求n的取值范围；
（3）若关于x的一元二次方程x2+mx﹣k=0（k为常数）在﹣2＜x＜3的范围内有解，求k的取值范围．

Answer 1

【答案】
（1）-2；（2，0）
（2）解：∵一元二次方程x2﹣2x=n有两个不相等的实数根，

∴△=4+4n＞0，

n＞﹣1

（3）解：一元二次方程x2﹣2x﹣k=0有解，

则△=4+4k≥0，

k≥﹣1，

方程的解为：x=1± ，

∵方程在﹣2＜x＜3的范围内有解，

1﹣ ＞﹣2，k＜8，

1+ ＜3，k＜3，

∴﹣1≤k＜8

【解析】解：（1）∵对称轴为直线x=1， ∴﹣ =1，m=﹣2，
则二次函数解析式为y=x2﹣2x，
x2﹣2x=0，x=0或2，
∴点A的坐标为 （2，0），
∴常数m=﹣2，点A的坐标为 （2，0）；
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．