题目内容
【题目】已知圆形纸片⊙O的直径为2，将其沿着两条互相垂直的直径折叠，得到四层的扇形，将最上的一层“撑”开来，“鼓”成一个无底的圆锥，则这个圆锥的高是（ ） 
A.
B.
C.
D.1
【答案】C
【解析】解：由题意知该无敌圆锥是由半圆O围成的，其半径为1，折叠后扇形的弧长为π， 设圆锥的底面半径为r，
则2πr=π，
解得：r= 
，
∴圆锥的高为 
= 
，
故选C．
【考点精析】利用圆锥的相关计算和翻折变换（折叠问题）对题目进行判断即可得到答案，需要熟知圆锥侧面展开图是一个扇形，这个扇形的半径称为圆锥的母线；圆锥侧面积S=πrl；V圆锥=1/3πR2h.；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
【题目】亚健康是时下社会热门话题，进行体育锻炼是远离亚健康的一种重要方式，为了解某市初中学生每天进行体育锻炼的时间情况，随机抽样调查了100名初中学生，根据调查结果得到如图所示的统计图表．
类别 | 时间t（小时） | 人数 |
A | t≤0.5 | 5 |
B | 0.5＜t≤1 | 20 |
C | 1＜t≤1.5 | a |
D | 1.5＜t≤2 | 30 |
E | t＞2 | 10 |
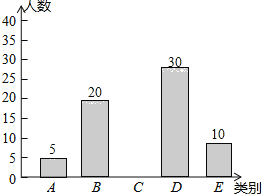
请根据图表信息解答下列问题：
（1）a= ；
（2）补全条形统计图；
（3）小王说：“我每天的锻炼时间是调查所得数据的中位数”，问小王每天进行体育锻炼的时间在什么范围内？
（4）据了解该市大约有30万名初中学生，请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数．
