题目内容
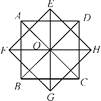
【题目】如图所示,点A是半圆上一个三等分点,点B是 ![]() 的中点,点P是直径 MN上一动点,若⊙O的直径为2,则AP+BP的最小值是 .
的中点,点P是直径 MN上一动点,若⊙O的直径为2,则AP+BP的最小值是 . 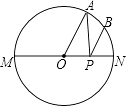
【答案】![]()
【解析】解:作点B关于MN的对称点B′,连接AB′交MN于点P,连接BP,此时AP+BP=AB′最小,连接OB′,如图所示. 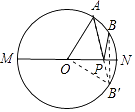
∵点B和点B′关于MN对称,
∴PB=PB′.
∵点A是半圆上一个三等分点,点B是 ![]() 的中点,
的中点,
∴∠AON=180°÷3=60°,∠B′ON=∠AON÷2=30°,
∴∠AOB′=∠AON+∠B′ON=90°.
∵OA=OB′=1,
∴AB′= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用圆心角、弧、弦的关系对题目进行判断即可得到答案,需要熟知在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目