题目内容
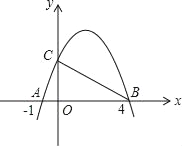
【题目】如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为﹣1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为_____.
【答案】(![]() ,
,![]() )
)
【解析】
连接AC,根据题意易证△AOC∽△COB,则![]() ,求得OC=2,即点C的坐标为(0,2),可设抛物线解析式为y=a(x+1)(x﹣4),然后将C点坐标代入求解,最后将解析式化为顶点式即可.
,求得OC=2,即点C的坐标为(0,2),可设抛物线解析式为y=a(x+1)(x﹣4),然后将C点坐标代入求解,最后将解析式化为顶点式即可.
解:连接AC,
∵A、B两点的横坐标分别为﹣1,4,
∴OA=1,OB=4,
∵∠ACB=90°,
∴∠CAB+∠ABC=90°,
∵CO⊥AB,
∴∠ABC+∠BCO=90°,
∴∠CAB=∠BCO,
又∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴![]() ,
,
即![]() =
=![]() ,
,
解得OC=2,
∴点C的坐标为(0,2),
∵A、B两点的横坐标分别为﹣1,4,
∴设抛物线解析式为y=a(x+1)(x﹣4),
把点C的坐标代入得,a(0+1)(0﹣4)=2,
解得a=﹣![]() ,
,
∴y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() (x2﹣3x﹣4)=﹣
(x2﹣3x﹣4)=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴此抛物线顶点的坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
相关题目