题目内容
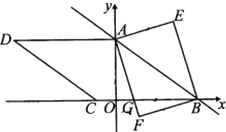
【题目】我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它由四个全等的直角三角形拼接而成．点E，F，G，H分别是AF，BG，CH，DE的中点，点M，N，P，Q分别是HE，EF，FG，GH上的中点，且四边形MNPQ是正方形，已知正方形ABCD的面积为20，则正方形MNPQ的面积是（ ）．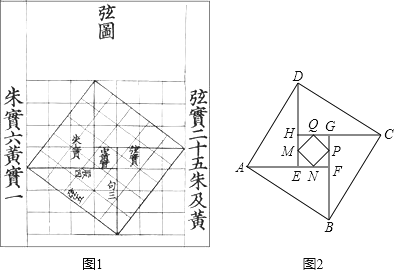
A.2B.1C.
D.
【答案】A
【解析】
由E为AF的中点，得到AE为AF的一半，由题意得到AE为DE的一半，根据正方形ABCD的面积求出边长，在直角三角形AED中，设AE=x，则DE=2x，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出正方形EFGH的边长，进而求出它的面积，根据正方形MNQP为正方形EFGH的中点四边形，面积为正方形EFGH的一半，求出即可．
∵E为AF的中点，DE=AF，
∴AE=
DE，
∵正方形ABCD面积为20，∴AD=2
，
在Rt△ADE中，设AE=x，则DE=2x，
根据勾股定理得：AD2=AE2+DE2，即20=x2+4x2，
解得：x=2，
∴AE=EF=2，
∴正方形EFGH的面积为4，
∵正方形MNQP为正方形EFGH的中点四边形，
∴正方形MNQP的面积为2．
故选：A
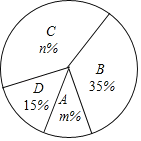
阅读快车系列答案
【题目】今年5月份，我市某中学开展争做“五好小公民”征文比赛活动，赛后随机抽取了部分参赛学生的成绩，按得分划分为A，B，C，D四个等级，并绘制了如下不完整的频数分布表和扇形统计图：
等级 | 成绩（s） | 频数（人数） |
A | 90＜s≤100 | 4 |
B | 80＜s≤90 | x |
C | 70＜s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息，解答以下问题：
（1）表中的x= ；
（2）扇形统计图中m= ，n= ，C等级对应的扇形的圆心角为 度；
（3）该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者，已知这四人中有两名男生（用a1，a2表示）和两名女生（用b1，b2表示），请用列表或画树状图的方法求恰好选取的是a1和b1的概率．
【题目】已知抛物线y=-x2-2x+c与x轴的一个交点是(1,0)．
（1）C的值为_______；
（2）选取适当的数据补填下表，并在平面直角坐标系内描点画出该抛物线的图像；
|
|
|
|
| |||
|
|
|
|
（3）根据所画图像，写出y>0时x的取值范围是_____．
