��Ŀ����
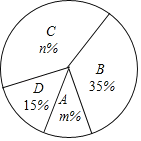
����Ŀ������5�·ݣ�����ij��ѧ��չ���������С�������ı���������������ȡ�˲��ֲ���ѧ���ijɼ������÷ֻ���ΪA��B��C��D�ĸ��ȼ��������������²�������Ƶ���ֲ���������ͳ��ͼ��
���ȼ� | ���ɼ���s�� | ��Ƶ���������� |
��A | ��90��s��100 | 4 |
��B | ��80��s��90 | x |
��C | ��70��s��80 | 16 |
��D | ��s��70 | 6 |
����������Ϣ������������⣺
��1�����е�x=�� ����
��2������ͳ��ͼ��m=�� ����n=�� ����C�ȼ���Ӧ�����ε�Բ�Ľ�Ϊ�� ���ȣ�
��3����У�����������A�ȼ�������ѧ����ѡȡ������ΪѧУ�����С����־Ը�ߣ���֪����������������������a1��a2��ʾ��������Ů������b1��b2��ʾ���������б�����״ͼ�ķ�����ǡ��ѡȡ����a1��b1�ĸ��ʣ�
���𰸡���1��14����2��10��40��144����3��ǡ��ѡȡ����a1��b1�ĸ���Ϊ![]() ��
��
����������1������D������������ռ�ٷֱȿɵ�������������������ȥ���������������ɵó�x��ֵ��
��2����A��C�����ֱ�������������A��C�İٷֱȼ��ɵ�m��n��ֵ������360������C�ȼ��ٷֱȿɵ��������
��3�����ȸ��������г�����Ȼ���ɱ���������еȿ��ܵĽ����ǡ��ѡȡ����a1��b1������������ø��ʹ�ʽ������ô𰸣�
��1���߱������ѧ��������Ϊ6��15%=40�ˣ�
��x=40����4+16+6��=14��
�ʴ�Ϊ��14��
��2����m%=![]() ��100%=10%��n%=
��100%=10%��n%=![]() ��10%=40%��
��10%=40%��
��m=10��n=40��
C�ȼ���Ӧ�����ε�Բ�Ľ�Ϊ360���40%=144�㣬
�ʴ�Ϊ��10��40��144��
��3���б����£�
a1 | a2 | b1 | b2 | |
a1 | a2��a1 | b1��a1 | b2��a1 | |
a2 | a1��a2 | b1��a2 | b2��a2 | |
b1 | a1��b1 | a2��b1 | b2��b1 | |
b2 | a1��b2 | a2��b2 | b1��b2 |
�ɱ���֪����12�ֵȿ��ܽ��������ǡ��ѡȡ����a1��b1����2�ֽ����
��ǡ��ѡȡ����a1��b1�ĸ���Ϊ![]() ��
��

 ��������ϵ�д�
��������ϵ�д�