题目内容
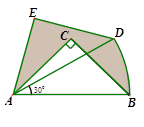
已知:如图,△ABC内接于⊙O,且AB=AC=13,BC=24,PA∥BC,割线PBD过圆心,交⊙O于另一个点D,联结CD.
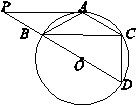
小题1:⑴求证:PA是⊙O的切线;
小题2:⑵求⊙O的半径及CD的长.

小题1:⑴求证:PA是⊙O的切线;
小题2:⑵求⊙O的半径及CD的长.
小题1:证明:(1)联结OA、OC,设OA交BC于G.

 ∵AB=AC,
∵AB=AC,∴
∴
 AOB=
AOB= AOC.
AOC.∵OB=OC,
∴OA⊥BC.
∴
 OGB=90°
OGB=90°∵PA∥BC,
∴
 OAP=
OAP= OGB=90°
OGB=90°∴OA⊥PA.
∴PA是⊙O的切线.
小题2:(2)∵AB=AC,OA⊥BC,BC="24 "
∴BG=
 BC=12.
BC=12.
∵AB=13,
∴AG=
 . …………………3分
. …………………3分设⊙O的半径为R,则OG=R-5.
在Rt△OBG中,∵
 ,
, .
. 解得,R=16.9 …
 ………………4分
………………4分∴OG=11.9.
∵BD是⊙O的直径,
∴O是BD中点,
∴OG是△BCD的中位线.
∴DC=2OG=23.8.
略

练习册系列答案
相关题目
 +
+
 于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):(6分)
于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):(6分)

 的度数
的度数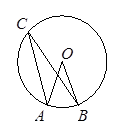
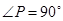 ,
,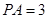 ,那么⊙O的
,那么⊙O的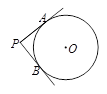
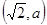 (a>0),半径为
(a>0),半径为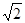 ,函数
,函数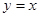 的图象被⊙P截得的弦AB的长为2.
的图象被⊙P截得的弦AB的长为2.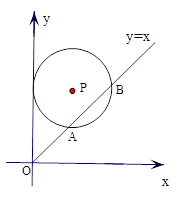
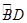 ,则图中阴影部分的面积是_________.
,则图中阴影部分的面积是_________.