题目内容
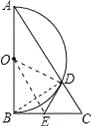
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
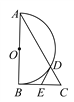
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
【答案】(1)证明见解析;(2) AD=6.
【解析】试题分析:(1)连接OD,OE,由AB为圆的直径得到三角形BCD为直角三角形,再由E为斜边BC的中点,得到DE=BE=DC,再由OB=OD,OE为公共边,利用SSS得到三角形OBE与三角形ODE全等,由全等三角形的对应角相等得到DE与OD垂直,即可得证;
(2)在直角三角形ABC中,由∠BAC=30°,得到BC为AC的一半,根据BC=2DE求出BC的长,确定出AC的长,再由∠C=60°,DE=EC得到三角形EDC为等边三角形,可得出DC的长,由AC﹣CD即可求出AD的长.
试题解析:(1)连接OD,OE,BD,
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
OB=OD,OE=OE,BE=DE,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,
∴BC=![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.

【题目】![]() 开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 | 1 | 2 | 3 | 4 | 5 | … |
电话费/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的关系式是什么?
(3)如果打电话超出![]() 分钟,需多付多少电话费?
分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是![]() 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟?