题目内容
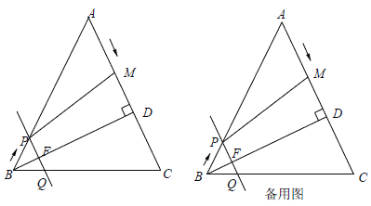
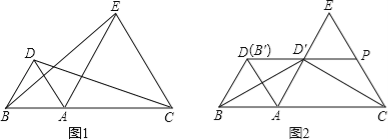
【题目】已知Rt△ABC中,∠ACB=90°,BC=6,∠A=30°,将△ABC绕点C逆时针旋转α,(0°<α≤60°),得到△DEC,设直线DE与直线AB相交于点P.
(1)如图1,连接PC,求证:PC平分∠EPA.
(2)如图2,在△ABC旋转过程中,连接BE,当△BCE的面积为9![]() 时,求α的度数.
时,求α的度数.
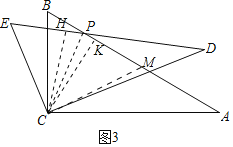
(3)如图3,当点P在边AB上时,问:PE+PB是否为定值?如果是,请求出此定值;如果不是,请说明理由.
【答案】(1)见解析;(2)α=60°;(3)PB+PE=6.
【解析】
(1)过C点作CN⊥DE于N,CF⊥AB于F,根据旋转前后三角形的面积不变作为相等关系得到CF=CN,从而判定PC平分∠EPA.
(2)如图2中,作EN⊥BC于N.利用三角形的面积公式构建方程求出sinα的值即可解决问题.
(3)如图3中,在PA上截取PM=PE连接CM,过C作CK⊥PA,CH⊥DE于H,连接PC.证明△PMC≌△PEC(SAS),CE=CM,PE=PM,推出PB+PE=BM,求出BM即可解决问题.
(1)过C点作CN⊥DE于N,CF⊥AB于F.
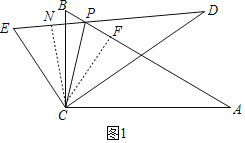
∵△ABC≌△DEC,
∴AB=DE.
∵S△ABC=![]() ABCF=S△DCE=
ABCF=S△DCE=![]() DECN,
DECN,
∵CF=CN,
∴PC平分∠EPA.
(2)如图2中,作EN⊥BC于N.
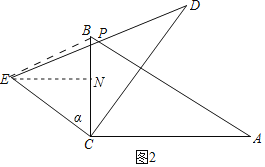
∵△BCE的面积为9![]() ,BC=EC=6,
,BC=EC=6,
∴![]() BCEN=9
BCEN=9![]() ,
,
∴![]() BCECsinα=9
BCECsinα=9![]() ,
,
∴sinα=![]() ,
,
∴α=60°.
(3)如图3中,在PA上截取PM=PE连接CM,过C作CK⊥PA,CH⊥DE于H,连接PC.
由(1)同理可证CP平分∠EPA,
∴∠EPC=∠APC,
∵PM=PE,PC=PC,
∴△PMC≌△PEC(SAS),
∴CE=CM,PE=PM.
又∵CE=CB,
∴CM=CB=6,且CK⊥PA,
∴K为BM的中点,即BK=![]() BM,
BM,
在Rt△BCK中,BK=BCcos60=6×![]() =3,
=3,
∴KM=BK=6,
∴PB+PE=PB+PM=BM=6.