Question

【题目】如图，在中，，于点，且，点分别从点向向匀速运动，速度均为;且运动过程中始终保持，直线交于点、交于点、交于点. 连接，设运动时间为.

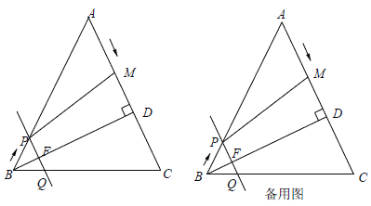
（1）当_____时，四边形是平行四边形.

（2）连接，，设的面积为，求与之间的函数关系式；

（3）是否存在某一时刻，使？若存在，求出的值;若不存在，说明理由；

（4）连接，是否存在某一时刻，使点在线段的垂直平分线上？若存在，请直接写出此时的值；若不存在，说明理由.

Answer 1

【答案】（1）2. 5；（2）；（3）；（4）存在，

【解析】

（1）假设PQCM为平行四边形，根据平行四边形的性质得到对边平行，进而得到AP=AM，列出关于t的方程，求出方程的解得到满足题意t的值；

（2）根据PQ∥AC可得△PBQ∽△ABC，根据相似三角形的形状必然相同可知△BPQ也为等腰三角形，即BP=PQ=t，再由证得的相似三角形得底比底等于高比高，用含t的代数式就可以表示出BF，进而得到三角形的高，又点M的运动速度和时间可知点M走过的路程AM=t，所以三角形的底CM=5-t．最后根据三角形的面积公式即可得到y与t的关系式；

（3）根据三角形的面积公式，先求出三角形ABC的面积，又根据第二问求出的y与t的解析式中列比例式求出t的值即可；

（4）假设存在，则根据垂直平分线上的点到线段两端点的距离相等即可得到MP=MC，过点M作MH垂直AB，由一对公共角的相等和一对直角的相等即可得到△AHM∽△ADB，由相似得到对应边成比例进而用含t的代数式表示出AH和HM的长，再由AP的长减AH的长表示出PH的长，从而在直角三角形PHM中根据勾股定理表示出MP的平方，再由AC的长减AM的长表示出MC的平方，根据两者的相等列出关于t的方程进而求出t的值．

（1）假设四边形PQCM是平行四边形，则PM∥QC，
∴AP：AB=AM：AC，

∵AB=AC，

∴AP=AM，即5-t=t，

解得：t=2.5，

∴当t=2.5时，四边形PQCM是平行四边形；

（2）∵PQ∥AC，AB=AC

∴△PBQ∽△ABC，

∴△PBQ为等腰三角形，PQ=PB=t，
∴，即，解得：BF=，

∴FD=BD-BF=4-，

又∵MC=AC-AM=5-t，

∴y=MCFD=（5-t）（4-）

即；

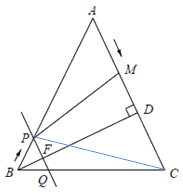
（3）存在；

∵S△ABC=ACBD=×5×4=10，

，

根据题意可得：

解得：t=2，或t=8，

∵8＞5，所以t=8不合题意，舍去

∴t=2；

（4）假设存在某一时刻t，使得M在线段PC的垂直平分线上，则MP=MC，

过M作MH⊥AB，交AB与H，如图所示：

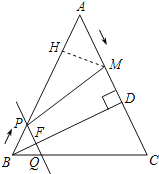
∵∠A=∠A，∠AHM=∠ADB=90°，

∴△AHM∽△ADB，

∴，

又∵AD=

∴ ，

∴HM=，AH=，
∴HP=5-t-=5-，
在Rt△HMP中，MP2=()2+(5-)2=t2-16t+25，

又∵MC2=（5-t）2=25-10t+t2，

∵MP2=MC2，
∴t2-16t+25=25-10t+t2

得t1＝ ，t2=0（舍去），
∴t=s时，点M在线段PC的垂直平分线上．