Question

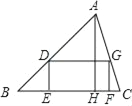
【题目】如图，△ABC是一块锐角三角形材料，高线AH长8cm，底边BC长10cm，要把它加工成一个矩形零件，使矩形DEFG的一边EF在BC上，其余两个顶点D、G分别在AB、AC上，AH交DG于M．

（1）求证：AMBC=AHDG；

（2）加工成的矩形零件DEFG的面积能否等于25cm2？若能，求出宽DE的长度；否则，请说明理由．

Answer 1

【答案】（1）详见解析；（2）加工成的矩形零件DEFG的面积不能等于25cm2，理由详见解析.

【解析】试题分析：（1）根据矩形的对边平行得到DG∥EF，利用“平行于三角形的一边的直线截其他两边或其他两边的延长线，得到的三角形与原三角形相似”得到△ADG∽△ABC，再根据相似三角形对应高的比等于相似比得到然后利用比例的基本性质即可证明AMBC=AHDG；
（2）当加工成的矩形零件DEFG的面积等于时,设宽DE的长度为xcm,则AM=(8x)cm, 根据（1）中结论AMBC=AHDG，列出方程整理得进而求解即可．

试题解析：(1)证明：∵四边形DEFG为矩形，

∴DG∥EF，

∴△ADG∽△ABC，

∴

∴AMBC=AHDG；

(2)加工成的矩形零件DEFG的面积不能等于，理由如下：

当加工成的矩形零件DEFG的面积等于时,设宽DE的长度为xcm,则AM=(8x)cm,

∵高线AH长8cm，底边BC长10cm，AMBC=AHDG，

∴

整理得

∵△=644×20=16<0，

∴x无实数根，

故加工成的矩形零件DEFG的面积不能等于.