题目内容
【题目】设二次函数y=ax2+bx+a-5（a、b为常数，a≠0），且2a+b=3.
（1）若该二次函数的图象经过点（-1,4），求该二次函数的解析式.
（2）无论a取何常数，这个二次函数的图象始终经过一个定点，求出这个定点坐标.
（3）已知点P（x0,m）和Q（1，n）都在二次函数的图象上，若x0＜1,且m>n，求x0的取值范围（用含a的代数式表示）。
【答案】（1）y=3x2-3x-2；（2）（1，-2）；（3）
（a>0）
【解析】
（1）将点（-1，4），即可求该二次函数的表达式
（2）将2a+b=3代入二次函数y=ax2+bx+a-5（a，b为常数，a≠0）中，整理得y=[ax2+（3-2a）x+a-3]-2=（ax-a+3）（x-1）-2，可知恒过点（1，2）；
（3）通过y=ax2+（3-2a）x+a-5，可求得对称轴为 
，因为x0＜1，且m＞n，所以只需判断对称轴的位置即可求x0的取值范围．
解：（1）∵函数y=ax2+bx+a-5的图象经过点（-1，4），且2a+b=3，
∴二次函数的解析式为y=3x2-3x-2；
（2）∵2a+b=3，
∴二次函数y=ax2+bx+a-5=ax2+（3-2a）x+a-5，
整理得，y=[ax2+（3-2a）x+a-3]-2=（ax-a+3）（x-1）-2
∴当x=1时，y=-2，
∴这个二次函数的图象始终经过一个定点，这个定点坐标为（1，-2）；
（3）∵y=ax2+（3-2a）x+a-5，
∴对称轴为
∵x0＜1，且m＞n，
∴当a＞0时，对称轴
解得：
当a＜0时，对称轴
解得：
（不符合题意，故x0不存在）
故x0的取值范围为：
【题目】已知函数y＝y1y2，其中y1＝
+1，y2＝
x﹣1，请对该函数及其图象进行如下探究：
解析式探究：根据给定的条件，可以确定出该函数的解析式为：______.
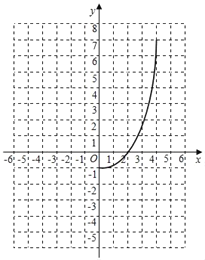
函数图象探究：①根据解析式，完成下表：
x | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | ﹣9 | ﹣ | m | n | ﹣1 | ﹣ | … |
m＝______，n＝_____.
②根据表中数据，在如图所示的平面直角坐标系中描点，并画出当x≤0时的函数图象；
结合画出的函数图象，解决问题：
①若A(x1，y1)、B(x2，y2)为图象上的两点，满足x1＜x2；则y1_____y2(用＜、＝、＞填空).
②写出关于x的方程y1y2＝﹣x+3的近似解(精确到0.1).