题目内容
【题目】已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),与y轴交于点B,且对称轴为x=1.
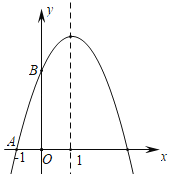
(1)求该抛物线的解析式;
(2)点P是抛物线对称轴上的一动点,当|PA﹣PB|取最大值时,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)P(1,6)
【解析】
(1)利用待定系数法即可求得;
(2)根据三角形两边之差小于第三边,得,当点P在直线AB上时,|PA﹣PB|最大,根据△ABO∽△APH求得PH的长度,即可求得P的坐标.
(1)由题意得: ,解得
,解得![]() ,
,
∴该抛物线的解析式:y=﹣x2+2x+3;
(2)∵抛物线为y=﹣x2+2x+3,
令x=0,则y=3,
∴B(0,3),
∵三角形两边之差小于第三边,
∴当点P在直线AB上时,|PA﹣PB|最大.
设抛物线的对称轴直线x=1与x轴交于点H,与直线AB交于点P,
∵PH∥y轴,
∴△ABO∽△APH
∴![]() ,
,
∴PH=2BO=6,
∴P(1,6)即为所求.


练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目