Question

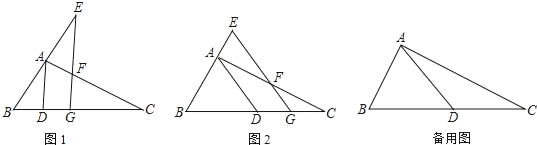
【题目】如图，已知矩形ABCD，AB＝6，AD＝2，对角线AC，BD交于点O，E为对角线AC上一点．

（1）求证：△OBC是等边三角形；

（2）连结BE，当BE＝时，求线段AE的长；

（3）在BC边上取点F，设P，Q分别为线段AE，BF的中点，连结EF，PQ．若EF＝2，求PQ的取值范围．

Answer 1

【答案】（1）详见解析；（2）当BE＝时，线段AE的长为3﹣1或3+1；（3）PQ的取值范围为≤PQ≤4．

【解析】

（1）根据矩形的性质可得：AD＝BC＝2，OA＝OC＝OB＝OD，∠ABC＝90°，然后利用勾股定理即可求出AC，从而求出OB、OC，即可证出△OBC是等边三角形；

（2）作BM⊥AC于M，先求出∠BAC，根据锐角三角函数，即可分别求出BM和AM，根据勾股定理即可求出EM，最后根据点E的位置分类讨论，即可求出AE的值；

（3）作EG⊥BC于G，作PN⊥BC于N，则EGPNAB，易知PN为梯形EABG的中位线，点N为BG的中点，设EG=x，根据题意，先求出x的取值范围，然后根据梯形中位线的性质和勾股定理分别求出PN和FG，从而求出QN，再根据勾股定理求出与x的函数关系式，根据一次函数的增减性即可求出的最值，从而求出PQ的取值范围.

（1）证明：∵四边形ABCD是矩形，

∴AD＝BC＝2，OA＝OC＝OB＝OD，∠ABC＝90°

∴AC＝＝＝4，

∴OB＝OC＝2，

∴OB＝OC＝BC，

∴△OBC是等边三角形；

（2）解：作BM⊥AC于M，如图1所示：

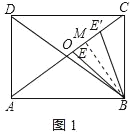
∵△OBC是等边三角形，

∴∠ACB＝60°，

∴∠BAC＝30°，

∴BM＝AB＝3，

∴AM＝BM＝3，EM＝＝＝1，

当点E在M的左侧时，AE＝AM﹣EM＝3﹣1；

当点E在M的右侧时，AE＝AM+EM＝3+1；

综上所述，当BE＝时，线段AE的长为3﹣1或3+1；

（3）解：作EG⊥BC于G，作PN⊥BC于N，则EGPNAB，

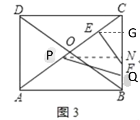
易知PN为梯形EABG的中位线，点N为BG的中点

设EG=x，当点E与C重合时，EG的最小值为0；如图所示EG≤EF=2，即0≤x≤2

∴PN=（EG+AB）＝，根据勾股定理：FG=

∵点Q、N分别为BF、BG的中点

∴BQ=BF，BN=BG

∴QN= BN－BQ=BG－BF=（BG－BF）=FG=，

∴

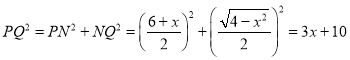
∵3＞0

∴随x的增大而增大

∴当x=0时，的最小值为10，当x=2时，的最大值为16

∴PQ的取值范围为≤PQ≤4．