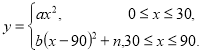Question

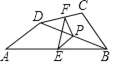
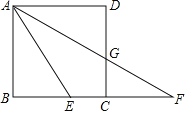
【题目】如图，点E是正方形ABCD的边BC上一点，连接AE，将线段AE绕点E顺时针旋转一定的角度得到EF，点C在EF上，连接AF交边CD于点G．

（1）若AB＝4，BF＝8，求CE的长；

（2）求证：AE＝BE+DG．

Answer 1

【答案】（1）EC＝1；（2）证明见解析.

【解析】

（1）设AE＝EF＝x，由正方形的性质可知BE＝8﹣x，AB＝4，在中，根据勾股定理可得x的值，易求CE的长；

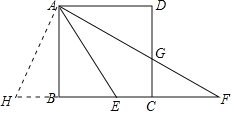
（2）延长EB到H，使得BH＝DG，则△ADG≌△ABE（SAS），由全等的性质及直角三角形的两锐角互余可证∠H＝∠EAH，根据等角对等边可知EA＝EH，易证结论.

（1）解：设AE＝EF＝x，

∵四边形ABCD是正方形，

∴∠ABE＝90°，AB＝BC＝4，

∵BF＝8，

∴CF＝8﹣4＝4，

∵BE＝BF﹣EF＝8﹣x，AB＝4，AE＝x，

∴x2＝42+（8﹣x）2，

∴x＝5，

∴EC＝EF﹣CF＝1．

（2）证明：延长EB到H，使得BH＝DG，则△ADG≌△ABE（SAS），

∴∠BAH＝∠DAG，

∴∠HAF＝∠BAD＝90°，

∵EF＝AE，

∴∠EAF＝∠F，

∵∠EAH+∠EAF＝90°，∠F+∠H＝90°，

∴∠H＝∠EAH，

∴EA＝EH，

∵EH＝BE+BH＝BE+DG，

∴AE＝BE+DG．