题目内容
【题目】如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC．若AC=6，则四边形ABCD的面积为 ．
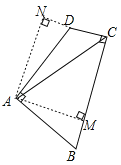
【答案】18．
【解析】
试题分析：如图，作AM⊥BC、AN⊥CD，交CD的延长线于点N；
∵∠BAD=∠BCD=90°，∴四边形AMCN为矩形，∠MAN=90°；
∵∠BAD=90°，∴∠BAM=∠DAN；
在△ABM与△ADN中，∵∠BAM=∠DAN，∠AMB=∠AND，AB=AD，∴△ABM≌△ADN（AAS），∴AM=AN（设为λ）；△ABM与△ADN的面积相等；
∴四边形ABCD的面积=正方形AMCN的面积；
由勾股定理得：AC2=AM2+MC2，而AC=6；
∴2λ2=36，λ2=18，故答案为：18．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
