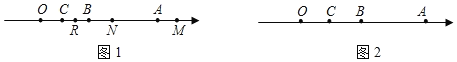题目内容
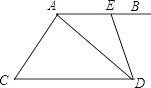
【题目】已知:点O为直线AB上一点,过点O作射线OC,使∠AOC=70°.
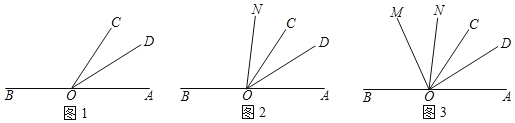
(1)如图1,若OD平分∠AOC,求∠DOB的度数;
(2)射线OM从OA出发,绕点O以每秒6°的速度逆时针旋转,同时,射线ON从OC出发绕点O以每秒4°的速度逆时针旋转,OM与ON同时出发(当ON首次与OB重合时,两条射线都停止运动),设运动的时间为t秒.
(i)如图2,在整个运动过程中,当∠BON=2∠COM时,求t的值;
(ⅱ)如图3,OP平分∠AOM,OQ平分∠BON,是否存在合适的t,使OC平分∠POQ,若存在,求出t的值,若不存在,请说明理由.
【答案】(1)145°;(2)(i)t![]() 或
或![]() ;(ⅱ)当t=3秒时,OC平分∠POQ.
;(ⅱ)当t=3秒时,OC平分∠POQ.
【解析】
(1)由角平分线定义求出∠AOD.再由平角求得∠BOD;
(2)(i)分两种情况:OM没超过OC时,OM超过OC时,列出t的方程,解方程便可得答案;
(ⅱ)由题意知OP在OQ的右边,据此画出草图,分别用t表示∠COP和∠COQ,由两角相等,列出t的方程进行解答便可.
(1)∵∠AOC=70°,OD平分∠AOC,∴∠AOD=35°,∴∠DOB=180°﹣∠AOD=145°;
(2)∵∠AOC=70°,∴∠BOC=180°﹣70°=110°,
(i)∵70°÷6![]() (秒),110°÷4
(秒),110°÷4![]() (秒)
(秒)
当0<t![]() 时,如图1,
时,如图1,
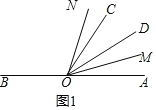
则∠BON=180°﹣70°﹣4t=110°﹣4t,∠COM=70°﹣6t.
∵∠BON=2∠COM,
∴110°﹣4t=2(70°﹣6t),
∴t![]() (秒);
(秒);
当![]() 时,如图2,
时,如图2,
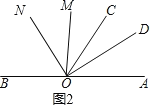
则∠BON=180°﹣70°﹣4t=110°﹣4t,∠COM=6t﹣70°.
∵∠BON=2∠COM,
∴110°﹣4t=2(6t﹣70°),
∴t![]() (秒)
(秒)
综上,t![]() 或
或![]() ;
;
(ⅱ)如图3,∠AOM=6t,∠BON=110°﹣4t,

∵OP平分∠AOM,OQ平分∠BON,
∴∠AOP=3t,∠NOQ=55°﹣2t,
∴∠COP=70°﹣3t,∠COQ=4t![]() (110°﹣4t)=55°+2t.
(110°﹣4t)=55°+2t.
∵OC平分∠POQ,
∴70°﹣3t=55°+2t,
∴t=3(秒),
∴当t=3秒时,OC平分∠POQ.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】“十一”期间沈阳世博园(10月1日)的进园人数为![]() 万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 |
|
|
|
|
|
|
(1)10月2日的进园人数是多少?
(2)10月1日-10月7日这7天内的进园人数最多的是哪天?最少的是哪天?它们相差多少?
【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由