题目内容
19、如图，已知平行四边形ABCD中，E是AB边的中点，DE交AC于点F，AC、DE把它分成的四部分的面积分别为S1S2S3S4，下面结论：①只有一对相似三角形
②EF：ED=1：2
③S1：S2：S3：S4=1：2：4：5
其中正确的结论是（ ）
分析：可知四边形ABCD是平行四边形，则AB∥CD，得到△AEF∽△CDF，且三角形的相似比是1：2，因而EF：FD=1：2，则EF：ED=1：3；且△ABC∽△CDA，S1：S3=1：4，且△AEF与△AED同底，高的比是1：3，则S2=2S1，同理S4=5S1∴S1：S2：S3：S4=1：2：4：5．
解答：解：①有两对相似三角形：
△AEF∽△CDF，△ABC∽△CDA，故该选项错误；
②∵AB∥CD，
∴AE：CD=EF：FD=1：2，故该选项错误；
③∵AB∥CD，
∴△AEF∽△CDF，
S1：S3=1：4，
又∵△AEF与△AED同底，高的比是1：3，
∴则S2=2S1
同理S4=5S1
∴S1：S2：S3：S4=1：2：4：5，
故该选项正确．故选B．
△AEF∽△CDF，△ABC∽△CDA，故该选项错误；
②∵AB∥CD，
∴AE：CD=EF：FD=1：2，故该选项错误；
③∵AB∥CD，
∴△AEF∽△CDF，
S1：S3=1：4，
又∵△AEF与△AED同底，高的比是1：3，
∴则S2=2S1
同理S4=5S1
∴S1：S2：S3：S4=1：2：4：5，
故该选项正确．故选B．
点评：本题运用了相似三角形的判定方法，及三角形相似的性质，面积的比等于相似比的平方．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．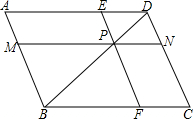
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．