Question

【题目】我校对全部900名学生就校园安全知识的了解程度，采用随机抽样调查的方式进行调查，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：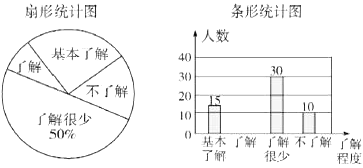

（1）接受问卷调查的学生共有人，条形统计图中“了解”部分所对应的人数是人；
（2）扇形统计图中“基本了解”部分所对应扇形的圆心角为°；
（3）若没有达到“了解”或“基本了解”的同学必须重新接受安全教育。 请根据上述调查结果估计我校学生中必须重新接受安全教育的总人数大约为人；
（4）若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请直接写出恰好抽到1个男生和1个女生的概率。

Answer 1

【答案】
（1）60；5
（2）90
（3）600
（4）

【解析】解：（1）∵“了解很少”的有30人，占50%，
∴接受问卷调查的学生共有：3050%=60（人）；
条形统计图中“了解”部分所对应的人数是60-15-30-10=5（人）.
故答案为：60；5.
（2）扇形统计图中“基本了解”部分所对应扇形的圆心角为：.
故答案为：90.
（3）抽查中除“了解”或“基本了解”的同学之外，有：60-15-5=40（人），
∴估计我校学生中必须重新接受安全教育的总人数大约为：900=600（人）.
故答案为：600.
（4）画树状图得：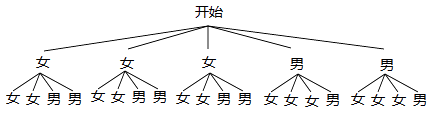

∵共有20种结果，它们出现的可能性相同，恰好抽到1个男生和1个女生的情况有12种，
∴恰好抽到1个男生和1个女生的概率为：=.
（1）由“了解很少”的有30人，占50%，可求得接受问卷调查的学生数，继而求得条形统计图中“了解”部分所对应的人数.
（2）由（1）可得扇形统计图中“基本了解”部分所对应扇形的圆心角.
（3）利用样本估计总体的方法，即可求得答案.
（4）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好抽到1个男生和1个女生的情况，再利用概率公式求解即可求得答案.