题目内容
【题目】在△ABC中，已知AC=5，且 
+ 
﹣ 
=0，则BC+AB=（ ）
A.6
B.7
C.8
D.9
【答案】B
【解析】解：如图：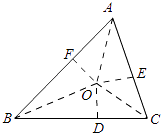 
作∠ABC，∠BCA，∠CAB的平分线相交于点O，过O作OD⊥BC，OE⊥AC，OF⊥AB，
设AF=m，BF=n，OD=OE=OF=r，
∴AE=m．BD=n，
∵AC=5，
∴CE=CD=5﹣m，
在RT△AOF中，tan∠BAO= 
，
∴ 
，
同理： 
， ，
∵ 
+ 
﹣ 
=0，
∴ 
，
∴n=1，
∴AB+BC=m+n+n+5﹣m=2n+5=7，
故选B
【考点精析】利用解直角三角形对题目进行判断即可得到答案，需要熟知解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
【题目】在不透明的袋子中有四张标着数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏． 小明画出树状图如图所示：
小华列出表格如下：
第一次 | 1 | 2 | 3 | 4 |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是，随机抽出一张卡片后（填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为；
（3）规定两次抽到的数字之和为奇数的获胜，你认为谁获胜的可能性大？为什么？
