题目内容
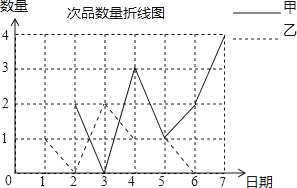
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?
【答案】(1)详见解析;(2)乙出现次品的波动小;(3)30.
【解析】
(1)根据平均数、众数、中位数的定义分别进行计算,即可补全统计图和图表;
(2)根据方差的意义进行判断,方差越大,波动性越大,方差越小,波动性越小,即可得出答案;
(3)根据图表中乙的平均数是1,即可求出乙加工该种零件30天出现次品件数.
(1):从图表(2)可以看出,甲的第一天是2,
则2出现了3次,出现的次数最多,众数是2,
把这组数据从小到大排列为0,1,2,2,2,3,4,最中间的数是2,
则中位数是2;
乙的平均数是1,则乙的第7天的数量是1×7﹣1﹣0﹣2﹣1﹣1﹣0=2;
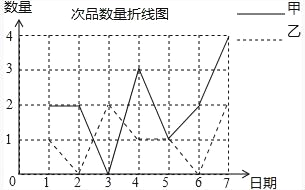
填表和补图如下:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 | 2 | 2 | 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
(2)∵S甲2=![]() ,S乙2=
,S乙2=![]() ,
,
∴S甲2>S乙2,
∴乙出现次品的波动小.
(3)∵乙的平均数是1,
∴30天出现次品是1×30=30(件).

练习册系列答案
相关题目