题目内容
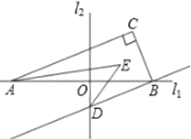
【题目】为倡导“低碳生活”,常选择以自行车作为代步工具.如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,车轮半径28cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2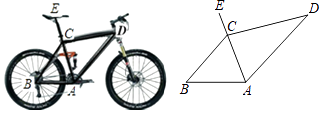
(1)求车座点E到地面的距离;(结果精确到1cm)
(2)求车把点D到车架档直线AB的距离.(结果精确到1cm).
【答案】
(1)解:作EF⊥AB于点F,如右图所示, 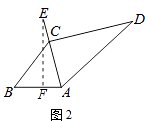
∵AC=45cm,EC=20cm,∠EAB=75°,
∴EF=AEsin75°=(45+20)×0.9659≈63cm,
即车座点E到车架档AB的距离是63cm,
∵车轮半径28cm,
∴车座点E到地面的距离是63+28=91cm
(2)解:作EF⊥AB于点F,如右图所示,
∵AC=45cm,EC=20cm,∠EAB=75°,
∴EF=AEsin75°=(45+20)×0.9659≈63cm,
即车座点E到车架档AB的距离是63cm.
【解析】作EF⊥AB于点F,先求得AE的长度,然后依据锐角三角函数的定义可求得EF的长,最后,依据车座点E到地面的距离是EF的长+轮半径的长求解即可;
(2)作DF⊥AB于点F,CG∥AB,CG与DF交与点G,先求得DG的长,然后再求得GF的长即可.

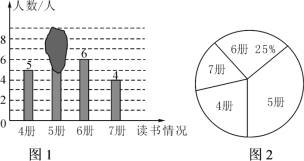
【题目】甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况绘制成如下不完整的统计图和表,依据图、表信息,解答下列问题:
相关统计量表:
量数 人 | 众数 | 中位数 | 平均数 | 方差 |
甲 |
|
| 2 |
|
乙 | 1 | 1 | 1 |
|
次品数量统计表:
天数 人 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 1 | 0 | 2 | 1 | 1 | 0 |
|
(1)补全图、表.
(2)判断谁出现次品的波动小.
(3)估计乙加工该种零件30天出现次品多少件?

【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?