题目内容
【题目】如图，转盘A中的6个扇形的面积相等，转盘B中的3个扇形的面积相等．分别任意转动转盘A、B各1次，当转盘停止转动时，将指针所落扇形中的2个数字分别作为平面直角坐标系中一个点的横坐标、纵坐标．
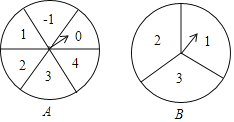
（1）用表格列出这样的点所有可能的坐标；
（2）求这些点落在二次函数y＝x2﹣5x+6的图象上的概率．
【答案】（1）见解析；（2）
【解析】
（1）根据题意列表，展示出所有等可能的坐标结果；
（2）由（1）可求得点落在二次函数y＝x2﹣5x+6的图象上的结果数，再根据概率公式计算即可解答．
（1）根据题意列表如下：
纵坐标 横坐标 | 3 | 1 | 2 |
﹣1 | （﹣1，3） | （﹣1，1） | （﹣1，2） |
0 | （0，3） | （0，1） | （0，2） |
1 | （1，3） | （1，1） | （1，2） |
2 | （2，3） | （2，1） | （2，2） |
3 | （3，3） | （3，1） | （3，2） |
4 | （4，3） | （4，1） | （4，2） |
由表可知，共有18种等可能的情况；
（2）由上表可知，点（1，2）、（4，2）都在二次函数y＝x2﹣5x+6的图象上，
所以P（这些点落在二次函数y＝x2﹣5x+6的图象上）＝
＝．
名校课堂系列答案
【题目】某公司推出一款产品，成本价10元/千克，经过市场调查，该产品的日销售量
（千克）与销售单价
（元/克）之间满足一次函数关系，该产品的日销售量与销售单价之间的几组对应值如下表：
销售单价 | 14 | 18 | 22 | 26 |
日销售量 | 240 | 180 | 120 |
|
（注：日销售利润=日销售量×（销售单价-成本单价））
（1）求关于的函数解析式（不要求写出的取值范围）；
（2）根据以上信息，填空：
①
_____元；
②当销售价格
_____元时，日销售利润
最大，最大值是______元；
（3）该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象，为了保证捐赠后每天的剩余利润不低于1025元，试确定该产品销售单价的范围．
