题目内容
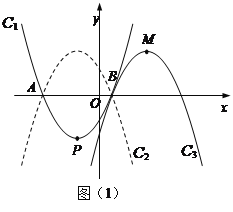
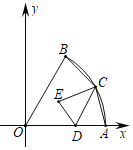
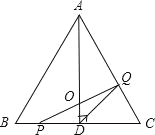
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P,Q分别从BC两点同时出发,其中点P沿BC向终点C运动.速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围.
【答案】(1)x=![]() ;(2)y
;(2)y![]() ;(3)当x=
;(3)当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,当0≤x<
时,以PQ为直径的圆与AC相切,当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.
【解析】
(1)若使PQ⊥AC,则当Q在AC上,根据路程=速度×时间表示出CP和CQ的长,再根据含30度的直角三角形的性质列方程求解;
(2)过点Q作QN⊥BC于N,利用三角函数求出QN,然后表示出DP,再根据三角形面积公式进行求解;
(3)可分点Q在AC和AB上两种情况讨论:当Q在AC时,根据(1)即可解决问题;当Q在AB上时,设以PQ为直径的圆与AC相切于点G,连接O′G,易证PQ=2O′G=QE+PF=![]() ,过点Q作QN⊥BC于N,在Rt△BNQ中,运用三角函数可得QN=
,过点Q作QN⊥BC于N,在Rt△BNQ中,运用三角函数可得QN=![]() ,BN=4x,则有PN=2x4,然后在Rt△QNP中,运用勾股定理即可解决问题.
,BN=4x,则有PN=2x4,然后在Rt△QNP中,运用勾股定理即可解决问题.
解:(1)当Q在AB上时,显然PQ不垂直于AC,
当Q在AC上时,由题意得,BP=x,CQ=2x,则PC=4x,
∵AB=BC=CA=4,
∴∠C=60°,
若PQ⊥AC,则有∠QPC=30°,
∴PC=2CQ,即4x=2×2x,
∴x=![]() ,
,
即当x=![]() 时,PQ⊥AC;
时,PQ⊥AC;
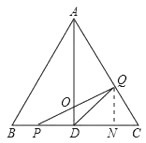
(2)如图,当0<x<2时,P在BD上,Q在AC上,过点Q作QN⊥BC于N,
∵∠C=60°,QC=2x,
∴QN=QC·sin60°=![]() ,
,
∵AB=AC,AD⊥BC,
∴BD=CD=![]() BC=2,
BC=2,
∴DP=2x,/span>
∴y=![]() PDQN=
PDQN=![]() ;
;
(3)显然,不存在x的值,使得以PQ为直径的圆与AC相离,
①当点Q在AC上时,由(1)可知,当x=![]() 时,以PQ为直径的圆与AC相切;
时,以PQ为直径的圆与AC相切;
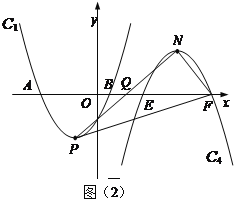
②当点Q在AB时,如图,
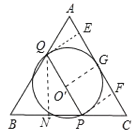
设以PQ为直径的圆与AC相切于点G,圆心为O′,连接O′G,则有O′G⊥AC,
过点Q作QE⊥AC于E,过点P作PF⊥AC于F,则QE∥O′G∥PF,
∵QO′=PO′,
∴EG=FG,
∴O′G=![]() (QE+PF),
(QE+PF),
∴PQ=2O′G=QE+PF,
由题意可得,CP=4x,AQ=2x4,
∴QE=AQsin60°=![]() ,PF=PCsin60°=
,PF=PCsin60°=![]() ,
,
∴PQ=![]() ,
,
过点Q作QN⊥BC于N,
在Rt△BNQ中,QN=BQsin60°=![]() ,BN=BQcos60°=
,BN=BQcos60°=![]() (82x)=4x,
(82x)=4x,
∴PN=x(4x)=2x4,
在Rt△QNP中,根据勾股定理可得: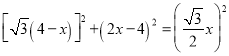 ,
,
整理可得:25x2160x+256=0,
解得:x1=x2=![]() ,
,
综上所述,当x=![]() 或
或![]() 时,以PQ为直径的圆与AC相切,当0≤x<
时,以PQ为直径的圆与AC相切,当0≤x<![]() 或
或![]() <x<
<x<![]() 或
或![]() <x≤4时,以PQ为直径的圆与AC相交.
<x≤4时,以PQ为直径的圆与AC相交.

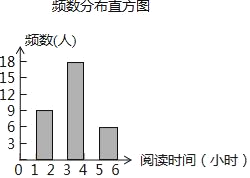
【题目】向阳中学为了解全校学生利用课外时间阅读的情况,调查者随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表(图).根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整;
(3)阅读时间不低于5小时的6人中,有2名男生、4名女生.现从这6名学生中选取两名同学进行读书宣讲,求选取的两名学生恰好是两名女生的概率.