题目内容
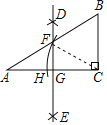
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
【答案】D
【解析】
先利用含30度的直角三角形三边的关系得AC=2![]() ,再利用基本作图得到FG垂直平分AC,CH=CF,则FA=FC,所以∠A=∠FCA=30°,接着证明△BCF为等边三角形,所以CF=CB=2,然后计算AC﹣CH即可.
,再利用基本作图得到FG垂直平分AC,CH=CF,则FA=FC,所以∠A=∠FCA=30°,接着证明△BCF为等边三角形,所以CF=CB=2,然后计算AC﹣CH即可.
在Rt△ABC中,∵∠A=30°,
∴∠B=60°,AC=![]() BC=2
BC=2![]() ,
,
由作法得FG垂直平分AC,CH=CF,
∴FA=FC,
∴∠A=∠FCA=30°,
∴∠BCF=60°,
∴△BCF为等边三角形,
∴CF=CB=2,
∴AH=AC﹣CH=2![]() ﹣2.
﹣2.
故选:D.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目