题目内容
【题目】某公司推出一款产品,成本价10元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/克)之间满足一次函数关系,该产品的日销售量与销售单价之间的几组对应值如下表:
(元/克)之间满足一次函数关系,该产品的日销售量与销售单价之间的几组对应值如下表:
销售单价 | 14 | 18 | 22 | 26 |
日销售量 | 240 | 180 | 120 |
|
(注:日销售利润=日销售量×(销售单价-成本单价))
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _____元;
_____元;
②当销售价格![]() _____元时,日销售利润
_____元时,日销售利润![]() 最大,最大值是______元;
最大,最大值是______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1025元,试确定该产品销售单价的范围.
【答案】(1)![]() ;(2)①60,②20,1500;(3)当
;(2)①60,②20,1500;(3)当![]() 时,捐赠后每天的剩余利润不低于1025元
时,捐赠后每天的剩余利润不低于1025元
【解析】
(1)从表格中取点代入一次函数解析式即可求解; (2)①由表格信息规律直接填写答案,或利用(1)中的函数解析式,求当![]() 时的函数值.②建立W与
时的函数值.②建立W与![]() 的函数关系式,利用二次函数性质求最大值即可.(3)先求捐赠后的利润为1025元时的销售单价,再利用二次函数的性质直接下结论即可;
的函数关系式,利用二次函数性质求最大值即可.(3)先求捐赠后的利润为1025元时的销售单价,再利用二次函数的性质直接下结论即可;
解:(1)设![]() 与
与![]() 的函数关系式为
的函数关系式为![]() ,
,
则![]() 解得:
解得:![]() ,
,![]() ,
,
![]() ,
,
(2)①因为![]() ,
,
所以当![]() 时,
时,![]() .
.
故答案为:![]() .
.
②因为![]() ,
,
所以当![]() 时,
时,![]() 有最大值,
有最大值,
最大值为![]() ,
,
故答案为20,1500
(3)因为![]() ,
,
整理得:![]() ,解得:
,解得:![]() ,
,![]()
所以,当![]() 时,捐赠后每天的剩余利润不低于1025元
时,捐赠后每天的剩余利润不低于1025元

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) | 售价(元) | 日销售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
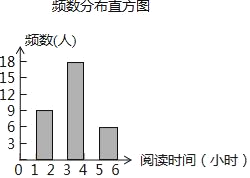
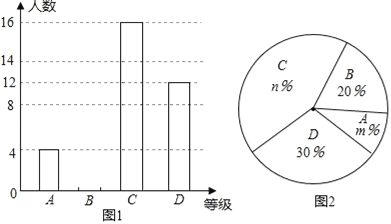
【题目】向阳中学为了解全校学生利用课外时间阅读的情况,调查者随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表(图).根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= ;
(2)将频数分布直方图补充完整;
(3)阅读时间不低于5小时的6人中,有2名男生、4名女生.现从这6名学生中选取两名同学进行读书宣讲,求选取的两名学生恰好是两名女生的概率.