Question

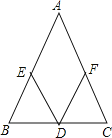
【题目】如图，已知.

（1）根据要求作图：在边上求作一点，使得点到、的距离相等，在边上求作一点，使得点到点、的距离相等；（不需要写作法，但需要保留作图痕迹和结论）

（2）在第（1）小题所作出的图中，求证：.

Answer 1

【答案】（1）作图见解析；（2）证明见解析.

【解析】

（1）到、的距离相等，则点D在的角平分线上，作的角平分线与BC的交点即为点D；到点、的距离相等，则点E在AD的垂直平分线上，作AD的垂直平分线与AB的交点即为点E；

（2）根据角平分线的性质和线段垂直平分线的性质可得∠CAD=∠ADE，再根据平行线的判定即可求解．

（1）解：如图所示：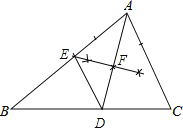

（2）证明：∵AD是∠BAC的角平分线，
∴∠CAD=∠BAD，
∵EF是AD的中垂线，
∴ED=EA，
∴∠ADE=∠BAD，
∴∠CAD=∠ADE，
∴DE∥AC．