题目内容
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,
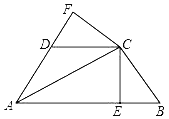
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求BE的长.
【答案】(1)见解析;(2)6
【解析】
(1)根据角平分线的性质可得:CE=CF,然后用HL即可证出Rt△BCE≌Rt△DCF;
(2)根据全等三角形的性质可得:BE=DF,然后利用HL证出Rt△CEA≌Rt△CFA,从而得出:AE=AF,从而求出BE的长.
(1)证明:∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,
在Rt△BCE和Rt△DCF中,
![]() ,
,
∴Rt△BCE≌Rt△DCF(HL);
(2)解:∵Rt△BCE≌Rt△DCF,
∴BE=DF,
在Rt△CEA和Rt△CFA中,
![]() ,
,
∴Rt△CEA≌Rt△CFA(HL),
∴AE=AF,
∴AB=AE+BE=AF+BE=AD+DF+BE=AD+2BE,
∴BE=![]() (AB﹣AD)=
(AB﹣AD)=![]() ×(21﹣9)=6.
×(21﹣9)=6.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目