题目内容
【题目】对于X,Y定义一种新运算F,F(X,Y)=aX+2bY﹣1(其中a,b均为非零常数),这里等式右边是通常的四则运算;例如:F(2,1)=2a+2b﹣1;
(1)F(1,1)=3,F(2,﹣1)=1;
①求a和b的值;
②若关于m的不等式组![]() 只有三个整数解,求实数k的取值范围;
只有三个整数解,求实数k的取值范围;
(2)若F(X,Y)=F(Y,X)对于任意实数X,Y都成立(这里F(X,Y)和F(Y,X)均有意义),求a与b满足的关系式.
【答案】(1)①a=2,b=1;②﹣9≤k<﹣5;(2)a=2b.
【解析】
(1)①根据定义的新运算T,列出二元一次方程组,解方程组求出a,b的值;
②根据(1)求出的a,b的值和新运算列出方程组求出m的取值范围,根据题意列出不等式,解不等式求出实数k的取值范围;
(2)根据新运算列出等式,得到(a-2b)(X-Y)=0,根据题意求出a,b应满足的关系式.
(1)①![]() ,
,
解得,![]() ;
;
②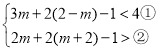 ,
,
解得![]() <m<1,
<m<1,
因为原不等式组有3个整数解,
所以﹣3≤![]() <﹣2,
<﹣2,
解得,﹣9≤k<﹣5;
(2)T(X,Y)=aX+2bY﹣1,T(Y,X)=aY+2bX﹣1,
所以aX+2bY﹣1=aY+2bX﹣1,
所以(a﹣2b)(X﹣Y)=0
所以a=2b.

练习册系列答案
相关题目