题目内容
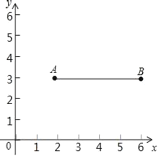
【题目】已知正方形ABCD中,点E,F分别为BC,CD上的点,连接AE,BF相交于点H,且AE⊥BF.
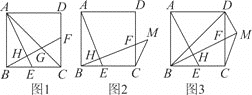
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
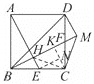
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)6.
【解析】
(1)根据正方形的性质得到∠ACB=∠ACD=45°,根据余角 的性质得到∠AEB=∠BFC,于是得到结论;
(2)过C作CK⊥BM于K,得到∠BKC=90°,推出四边形ABCD是正方形,根据正方形的性质得到AB=BC,∠ABC=∠BCD=90°,得到∠ABH=∠BCK,在△ABH根据全等三角形的性质即可得到结论;
(3)过E作EN⊥CK于N,得到四边形HENK是矩形,根据矩形的性质得到HK=EN=BH,∠BHE=∠NEC,根据全等三角形的性质得到HE=CN=NK=1,求得CK=BH=2,得到BM=6,连接CH,根据全等三角形的性质得到BH=DM=2,∠BHC=∠DMC=135°.求得∠DMB=90°,于是得到结论.
(1)∵四边形ABCD是正方形,∴∠ABC=∠BCD=90°,
∴∠ACB=∠ACD=45°,
∵AE⊥BF,
∴∠AEB+∠FBC=90°,
∵∠FBC+∠BFC=90°,
∴∠AEB=∠BFC,
∵∠AGF=∠BFC+∠ACF,
∴∠AGF=∠AEB+45°.
(2)过C作CK⊥BM于K,
∴∠BKC=∠AHB=90°,
∵∠BMC=45°,
∴CK=MK,
∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABH=∠BCK,
∴△ABH≌△BCK(AAS),
∴BH=CK=MK,AH=BK,∴BM=BK+MK=AH+BH.
(3)由(2)得,BH=CK=MK,∵H为BM的三等分点,
∴BH=HK=KM,
过E作EN⊥CK于N,∴四边形HENK是矩形,
∴HK=EN=BH,∠BHE=∠ENC,∴△BHE≌△ENC(ASA),
∴HE=CN=NK=1,∴CK=BH=2,
∴BM=6,
连接CH,
∵HK=MK,CK⊥MH,∠BMC=45°,∴CH=CM,∠MCH=90°,
∴∠BCH=∠DCM,∴△BHC≌△DMC(SAS),
∴BH=DM=2,∠BHC=∠DMC=135°,
∴∠DMB=90°,
∴△BDM的面积为![]() DM·BM=6.
DM·BM=6.