题目内容
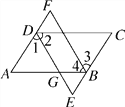
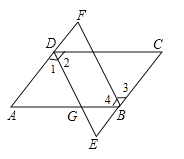
【题目】(南阳唐河县期中)如图,在ABCD中,DE平分∠ADC交AB于G,交CB的延长线于E,BF平分∠ABC交AD的延长线于F.
(1)若AD=5,AB=8,求GB的长;
(2)求证:∠E=∠F.
【答案】(1)3;(2)见解析
【解析】试题分析:(1)直接利用平行四边形的性质结合角平分线的性质得出∠2=∠AGD,进而得出AD=AG,得出答案即可;
(2)根据平行四边形的性质可得AF∥CE,根据平行四边形的性质和角平分线定义证明∠2=∠4,然后再证明ED∥FB,根据两组对边分别平行的四边形是平行四边形可得四边形BFDE是平行四边形,进而得出答案.
试题解析:(1)解:∵在ABCD中,DE平分∠ADC交AB于点G,BF平分∠ABC交AD的延长线于F,∴∠1=∠2,∠3=∠4,AB∥DC,∴∠2=∠AGD,∴∠1=∠AGD,∴AD=AG=5.∵AB=8,∴BG=8﹣5=3;
(2)证明:∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,DC∥AB,AD∥BC.∵DE平分∠ADC,∴∠2=![]() ∠ADC.∵BF平分∠ABC,∴∠4=
∠ADC.∵BF平分∠ABC,∴∠4=![]() ∠ABC,∴∠2=∠4.∵DC∥AB,∴∠AGD=∠2,∴∠AGD=∠4,∴ED∥FB.∵AF∥CE,∴四边形BFDE是平行四边形,∴∠E=∠F.
∠ABC,∴∠2=∠4.∵DC∥AB,∴∠AGD=∠2,∴∠AGD=∠4,∴ED∥FB.∵AF∥CE,∴四边形BFDE是平行四边形,∴∠E=∠F.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目